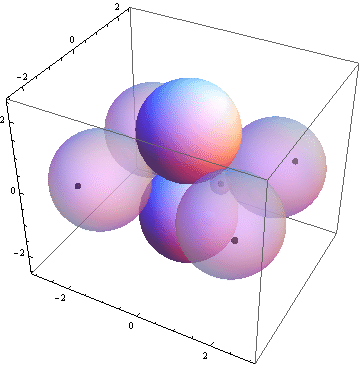(* H2C=CH2 with spherical bananas: Two fused methanes with CH4 data CH4Mt(min).nb 28.12.2012 *)
Clear[z,sig1,sig2,sig4,k1,k2,k4,nc,R1,R2,R3,R4,w,p,vee,vne,vnn,
xc,yc,zc,xn,yn,zn,oc,ch,rr,cs,ss,d1,d2,d3,d4,d5,pi,i,j,d,t];
z=6.0;
pi=0.0; (* distance of bananas from C-C axis, pi =0 is regular tetraedric *)
nc=8; (* number of clouds *)
sig1=0.3; sig2=0.3; sig4=sig2; (* screening const. from e-e interaction in doubly occ. clouds *)
k1=1.027; k2=1.23; k4=k2; (* parameters for kinetic energy of clouds; k=1.0 Kimball's lowest value *)
bohr=0.529177; rad=57.29578;
(* C He-shells *)
Ekin = 2*(2.25*k1/R1^2);
vee=2*(3.0*sig1/R1);
vne=-2*(3.0*z/R1);
(* this is the common edge assumption *)
R4=R2;
(* bonding pairs *)
Ekin = Ekin + 2.25*(4*k2/R2^2+2*k4/R4^2);
vee=vee+3.0*(4*sig2/R2+2*sig4/R4);
(* cloud occupation *)
oc={-2,-2,-2,-2,-2,-2,-2,-2};
(* nuclear charges for C1,C2,H3,H4,H5,H6, banana7, banana8 *)
ch={6,6,1,1,1,1,0,0};
(* cloud radii in the same order *)
rr={R1,R1,R2,R2,R2,R2,R4,R4};
(* w is half angle between two C-H of CH4, i.e. 109.47°/2 *)
w=ArcCos[-1/3]/2;
cs=Cos[w]; ss=Sin[w];
(* edge length of tetrahedron of 4 equal clouds *)
a=4*(R1+R2)/Sqrt[6]; (* 4/Sqrt[6] is also Sqrt[8/3] *)
(* x is C-C bond axis, xy plane of molecule *)
(* nuclear coordinates in terms of radii; C nucleus assumed in center of C(1s) cloud *)
d1=(R1+R2)*cs; (* R1+R2 is radius of outer sphere for tetrahedron of equal clouds *)
d2=d1+(R1+R2+p)*cs; d3=(R1+R2+p)*ss;
xn={-d1,d1,-d2,-d2,d2,d2,0,0};
yn={0,0,d3,-d3,-d3,d3,0,0};
zn={0,0,0,0,0,0,0,0};
(* cloud coordinates in terms of radii *)
d4=d1+(R1+R2)*cs; d5=(R1+R2)*ss;
xc={-d1,d1,-d4,-d4,d4,d4,0,0};
yc={0,0,d5,-d5,-d5,d5,0,0};
zc={0,0,0,0,0,0,pi+a/2,-pi-a/2};
(* potential energy of protons in CH-clouds with eccentricity p *)
vne=vne-4*(3-(p/R2)^2)/R2;
(* cc: sum of cloud-cloud potential energies *)
For[i = 1, i < nc, i++,
For[j = i+1, j < nc+1, j++,
vee = vee + oc[[i]]*oc[[j]]/Sqrt[(xc[[i]]-xc[[j]])^2+(yc[[i]]-yc[[j]])^2+(zc[[i]]-zc[[j]])^2]]]
(* nn: sum of nuclei-nuclei potential energies *)
vnn = 0.0;
For[i = 1, i < nc-2, i++,
For[j = i+1, j < nc-1, j++,
vnn = vnn + ch[[i]]*ch[[j]]/Sqrt[(xn[[i]]-xn[[j]])^2+(yn[[i]]-yn[[j]])^2]]]
(* cn: sum of cloud-nuclei potential energies *)
For[i = 1, i < nc+1, i++,
For[j = 1, j < nc+1, j++,
If[i != j,
vne = vne + oc[[i]]*ch[[j]]/Sqrt[(xc[[i]]-xn[[j]])^2+(yc[[i]]-yn[[j]])^2+(zc[[i]]-zn[[j]])^2]]]]
Epot=vne+vee+vnn;
func=Ekin+Epot;
(* results of CH4 computation; if this is not available, decomment the minimize function *)
(* R1=0.2623610; R2=1.2461360; p=0.53986226; *)
(* minimization function for R1, R2, p *)
t = FindMinimum[func,{R1,0.26},{R2,1.24},{p,0.54},{Method -> Automatic}, {MaxIterations -> 500}]
(* func *)
vne /. t[[2]]
vee /. t[[2]]
vnn /. t[[2]]
-Epot/Ekin /. t[[2]]
2*d1*bohr /. t[[2]]
(R1+R2+p)*bohr /. t[[2]]
(R1+R2)*bohr /. t[[2]]
2*w*rad /. t[[2]]
4*(R1*(R1+2*R4))^(3/2)/(R1+R4)^3 /. t[[2]]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
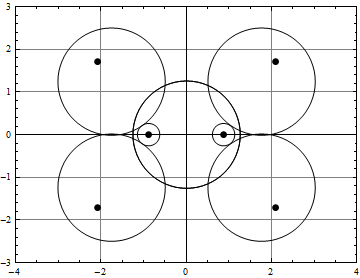
(* projection on xy-plane of molecule *)
plot1=Graphics[{Circle[{xc[[1]],yc[[1]]},R1], Circle[{xc[[2]],yc[[2]]},R1],Circle[{xc[[3]],yc[[3]]},R2],Circle[{xc[[4]],yc[[4]]},R2],Circle[{xc[[5]],yc[[5]]},R2],Circle[{xc[[6]],yc[[6]]},R2],Circle[{xc[[7]],yc[[7]]},R4],Circle[{xc[[8]],yc[[8]]},R4],Disk[{xn[[1]],yn[[1]]},0.08], Disk[{xn[[2]],yn[[2]]},0.08], Disk[{xn[[3]],yn[[3]]},0.08], Disk[{xn[[4]],yn[[4]]},0.08],Disk[{xn[[5]],yn[[5]]},0.08],Disk[{xn[[6]],yn[[6]]},0.08]} ] /. t[[2]];
Show[plot1,{AspectRatio → Automatic,Axes -> True,GridLines -> Automatic, PlotRange → {{-4,4},{-3,3}}, Frame -> True}]
(* 3D projection of molecule *)
plot1=Graphics3D[{{Opacity[0.5],Sphere[{xc[[1]],yc[[1]],0},R1], Sphere[{xc[[2]],yc[[2]],0},R1],Sphere[{xc[[3]],yc[[3]],0},R2],Sphere[{xc[[4]],yc[[4]],0},R2],Sphere[{xc[[5]],yc[[5]],0},R2],Sphere[{xc[[6]],yc[[6]],0},R2]},{Darker[Red,1],Sphere[{xn[[1]],yn[[1]],0},0.08],Sphere[{xn[[2]],yn[[2]],0},0.08], Sphere[{xn[[3]],yn[[3]],0},0.08], Sphere[{xn[[4]],yn[[4]],0},0.08],Sphere[{xn[[5]],yn[[5]],0},0.08],Sphere[{xn[[6]],yn[[6]],0},0.08]},Sphere[{xc[[7]],yc[[7]],zc[[7]]},R4],Sphere[{xc[[8]],yc[[8]],zc[[8]]},R4] }] /. t[[2]];
Show[plot1,{AspectRatio → Automatic,Axes -> True}]
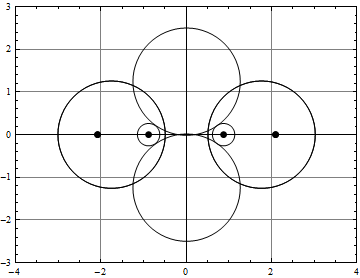
(* projection on xz-plane, perpendicular to molecular plane *)
plot2=Graphics[{Circle[{xc[[1]],zc[[1]]},R1], Circle[{xc[[2]],zc[[2]]},R1],Circle[{xc[[3]],zc[[3]]},R2],Circle[{xc[[4]],zc[[4]]},R2],Circle[{xc[[5]],zc[[5]]},R2],Circle[{xc[[6]],zc[[6]]},R2],Circle[{xc[[7]],zc[[7]]},R4],Circle[{xc[[8]],zc[[8]]},R4],Disk[{xn[[1]],zn[[1]]},0.08], Disk[{xn[[2]],zn[[2]]},0.08], Disk[{xn[[3]],zn[[3]]},0.08], Disk[{xn[[4]],zn[[4]]},0.08],Disk[{xn[[5]],zn[[5]]},0.08],Disk[{xn[[6]],zn[[6]]},0.08]} ] /. t[[2]];
Show[plot2,{AspectRatio → Automatic,Axes -> True,GridLines -> Automatic, PlotRange → {{-4,4},{-3,3}}, Frame -> True}]