LiH, BeH2, BH3, CH4 molecules: In preparation

Similar to Li₂ the LiH molecule with non overlapping clouds is shown here. This and the internal on the right are parametrized with the same RHF/6-311G optimized Etot, Vne, Vee and Re values. The table below gives the fitted Kimball values of these quantities for the two models. The bond length is nearly the same as can be seen in the figures:

This is the internal cloud model using Li(1s²,2s) and a small exchange correction for the overlapped clouds. It is interesting to compare the parameter values. For the internal model the parameter for the Li-H cloud assumes a value below 1.0 - Kimballs parameter - which is connected to the principle quantum number n=2.

Comparison
Method	Etot Eh	dLiH Å	Vne Eh	Vee Eh	Vnn Eh	D0 eV
RHF/6-311G** opt	-8.022475	1.5941	-20.42077	3.469247	0.9959	-
LiH, left model	-8.02263	1.5949	-20.4953	3.45468	0.9954	-
LiH, right model	-8.03042	1.58112	-20.5058	3.44093	1.00405	-
Experiment	na	1.5957	na	na	na	2.42871

Parameters fitted
Method	k1	k2	sigma1	sigma2	exchange correction
LiH, left model	1.028055	1.232586	0.274383	0.299973	-
LiH, right model	1.016140	0.658581	0.257422	0.229589	-2.6034 mEh
Kimball/Slater	1.0	1.0	0.3	0.3	-

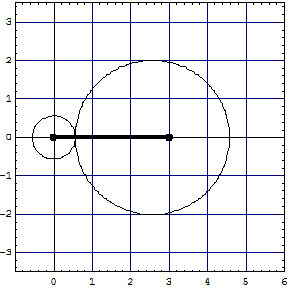
BeH2

We continue with "sp" type BeH2: Left image with non overlapped clouds, no exchange correction, same size and similar energy terms as the right model:

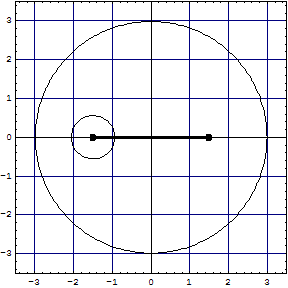
The overlapped model has now two volumes with exchange corrections, the smaller spherical inside the lens shaped volume between the two sp-clouds. The lens has not yet been exchange corrected. With Wolfram CDF Player (free plugin to your browser) you can turn the model and inspect the overlap regions:

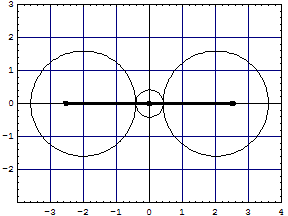
BH3

For "sp2" like BH3 with non overlapped clouds we get a non tangent (!) model:

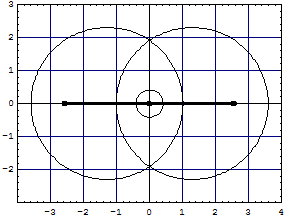
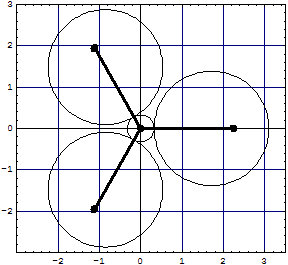and for the overlapped model we have now three exchange lenses with 8 electrons in the core region (6 excluded!) and 6 or 4 around it, not yet corrected:

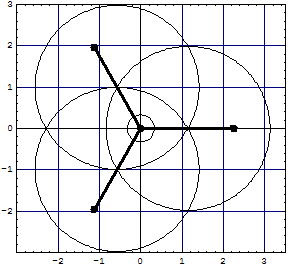
CH4

The non overlapped "sp3" like CH4 is seen from the apex on a C3 axis. It has tangent CH clouds in this parametrization. The projection into the base plane makes the CH bonds appear overlapping the core.

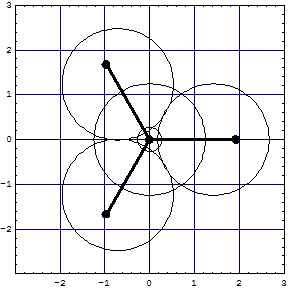
The overlapped model has 6 lens shaped overlap regions and 10 electrons in the core region (8 excluded!). In the surrounding sixfold overlap 8 electrons roam about, whose cohabitation has not been allowed by Pauli! Inspect them with the Wolfram CDF Player.

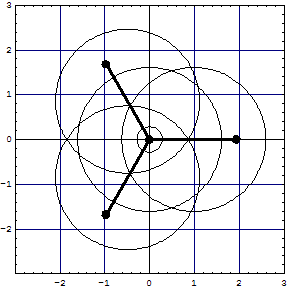
For LCAO-MO and Hybridization fans:

Hybridization is a tool of the computational chemists to construct symmetry adapted orthogonal orbitals from (spherical) atomic orbitals. Chemists who use "hybridization" as a qualitative visualization tool (which they shouldn't), will recognize, that the left series of Kimball model projections is similar (except for the spherical shape of the Kimball clouds) to what they construct as hybrids of atomic s and p orbitals. It is important to realize, that there is no hybridization scheme applied to Kimballs model to arrive at this similarity. This becomes obvious when you are studying the (simple!) calculations. The energy minimalization of the sum of kinetic energy and elctrostatic potential terms just leads to these results, reflecting the structure defined by the potential of the nuclear frame. It is also visible, that the equilibrium assembly of the clouds and nuclei produces an "orthogonal" set. This means that the clouds do not (or very slightly) overlap. There are, of course, no vanishing "overlap integrals" with 3-D charge clouds

which penetrate each other in real space. Charge densities do not subtract! But atomic s and p orbitals are orthogonal wavefunctions and thus have vanishing overlap (= product) integrals (over all space). This does not apply to Kimballs model. The clouds are not orbitals but relate to the ψ² amplitude distributions which have the same sign everywhere.- I'd like to point out an important fact rarely explained in Chemistry texts and so obvious when using Kimballs model: The (crude, qualitative) LCAO-MO constructions, and similarly the VB-hybridization schemes used in textbooks and even in the research literature, are always shown and discussed before the compulsary antisymmetrization is done, i.e. the exclusion of Pauli forbidden multiple electron occupations. If the wavefunctions thus "constructed" are not checked for being orthogonal, that gives an incorrect idea about the electron density distribution in the bonding region.