Structure - Energy
Thousands of molecular structures exist in many repositories, to be downloaded. "If you have the structure, you have the energy" (Linus Pauling). For a quantum chemical computation you need as input a reasonable set of atomic coordinates to start with. The "model chemistry" then defines the QC approximation and basis set to be applied. The first result, if converged, gives the energy and its components for the original structure input. Often an optimized structure consistent with the model is then attempted. Hopefully, this is not much different from the (high quality) experimental structure at start.
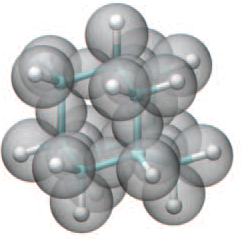
About 1961, we proposed to André Dreiding, then perfecting the "Dreiding Model" set, to apply Kimball's model to extract energy differences of molecular conformations, intensely discussed at that time. Just take a ruler and measure the distances between e.g. C-methyl and the atomic frame in the molecular vicinity, rotated by the conformational change to be examined. The (periodic) change of distances by rotations of the vertices of Dreiding's model around the bond in question seemed to be precise enough to allow calculation of rough energy differences between staggered, eclipsed, gauche a.o. conformations. This worked (but was never published).
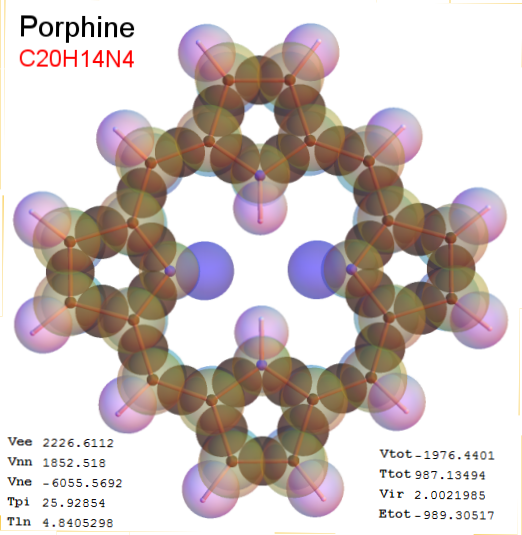
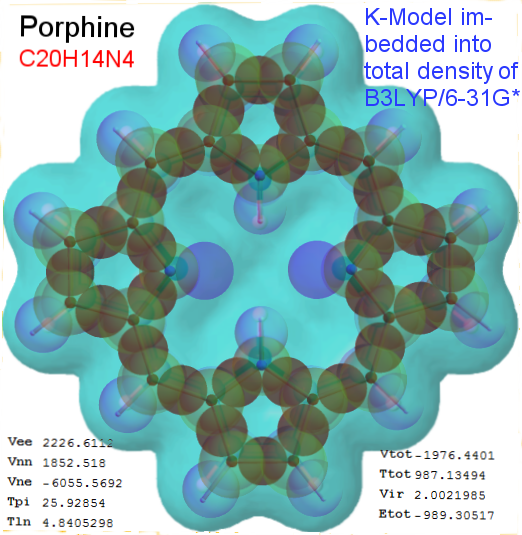
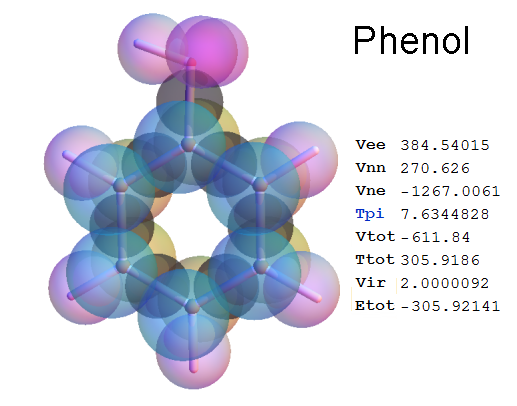
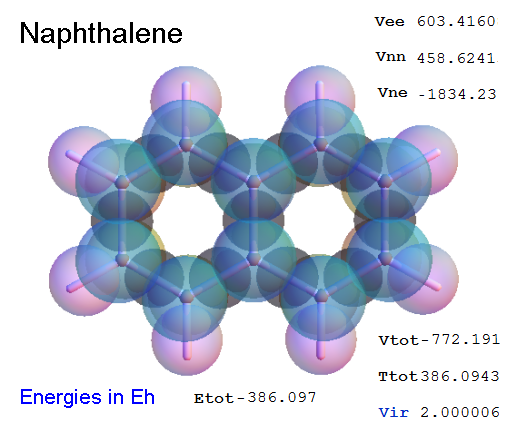
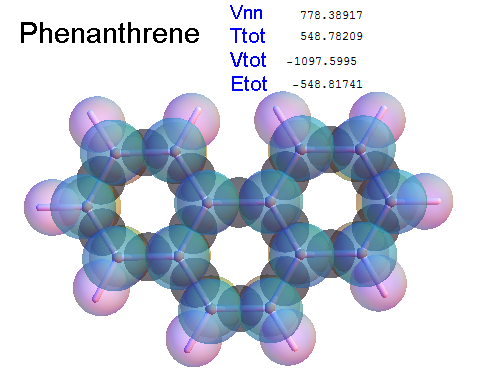
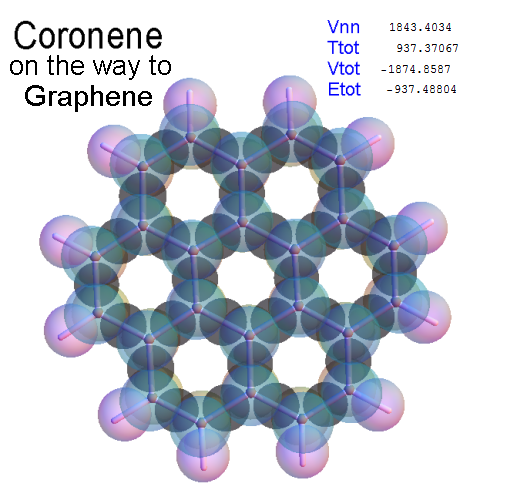
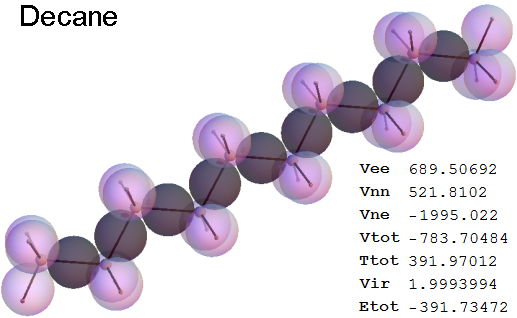
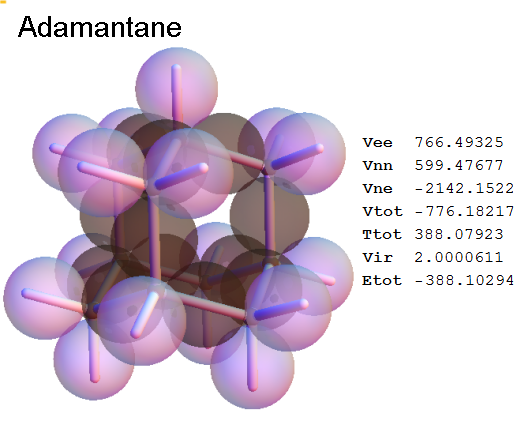
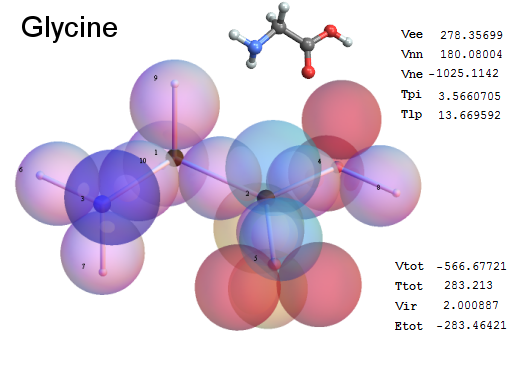
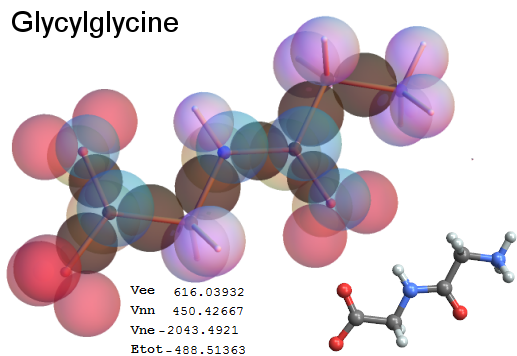
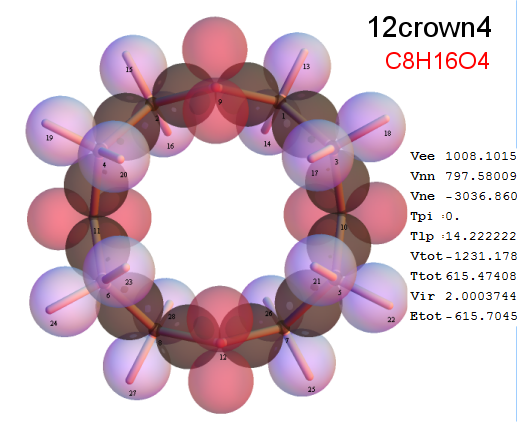
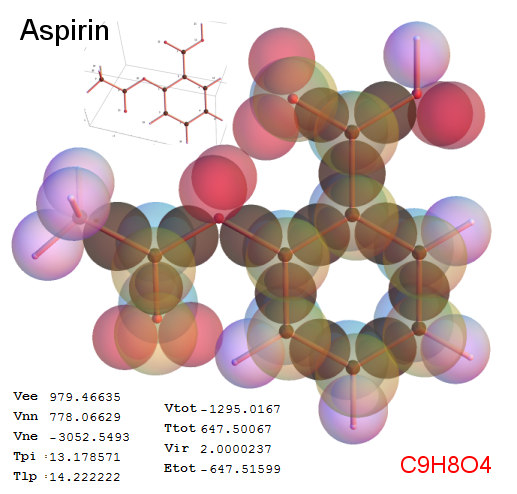
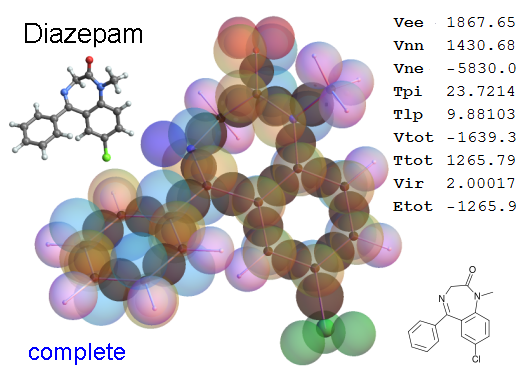
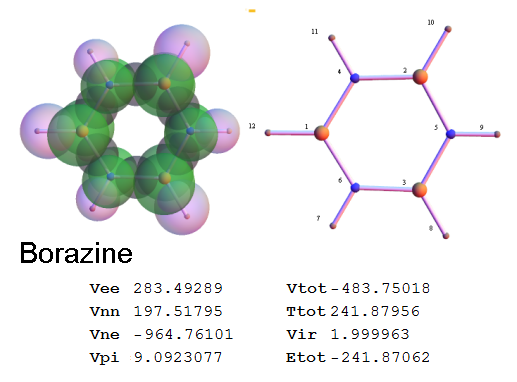
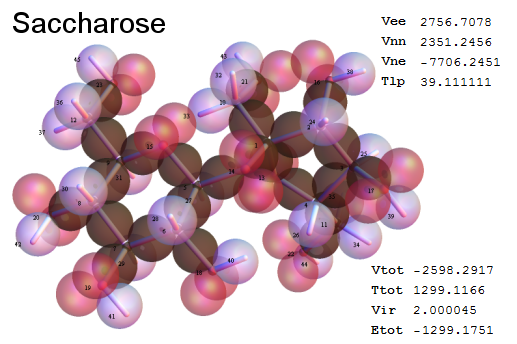
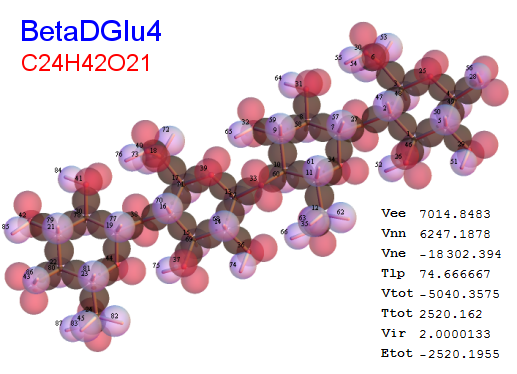
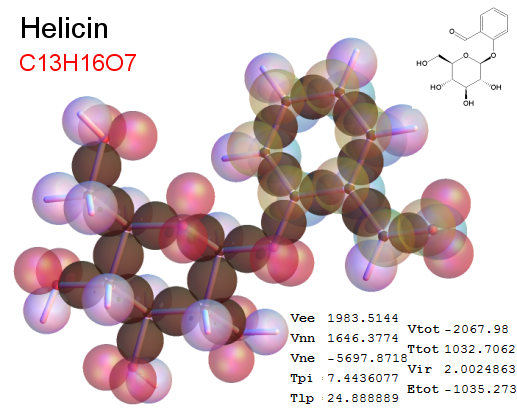
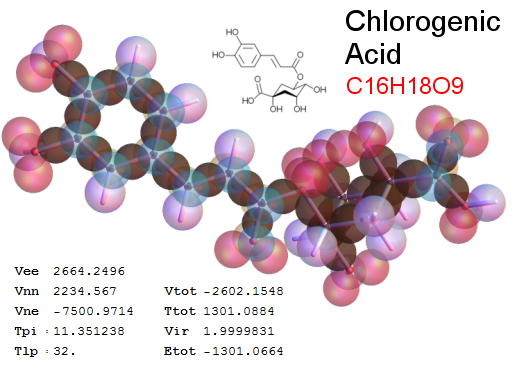
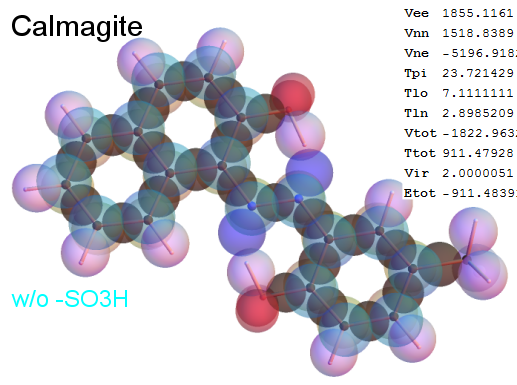
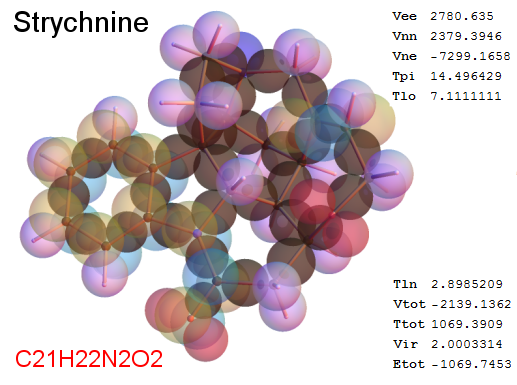
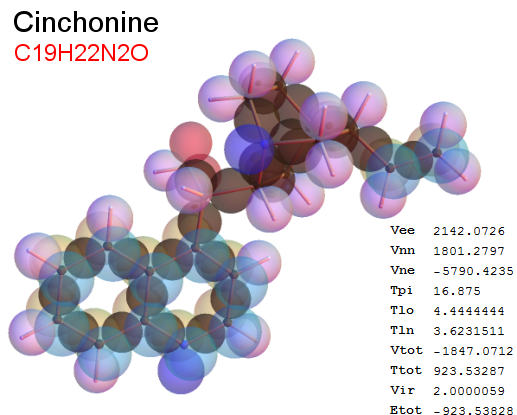
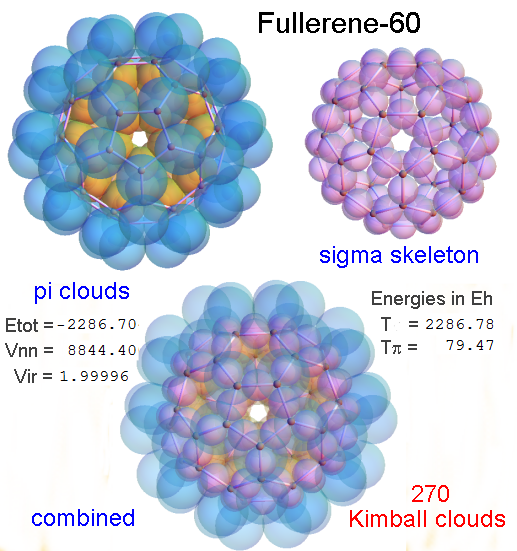
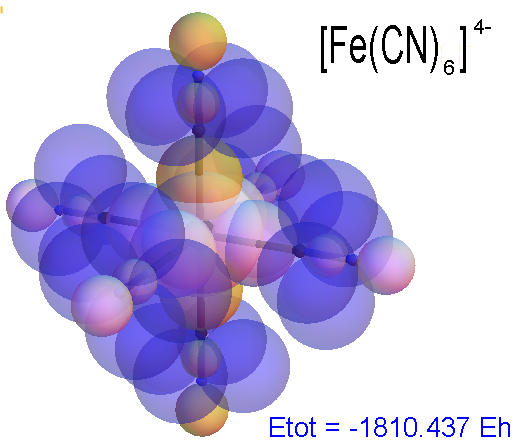
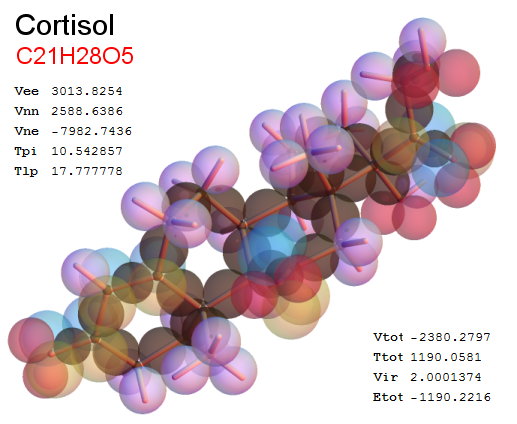
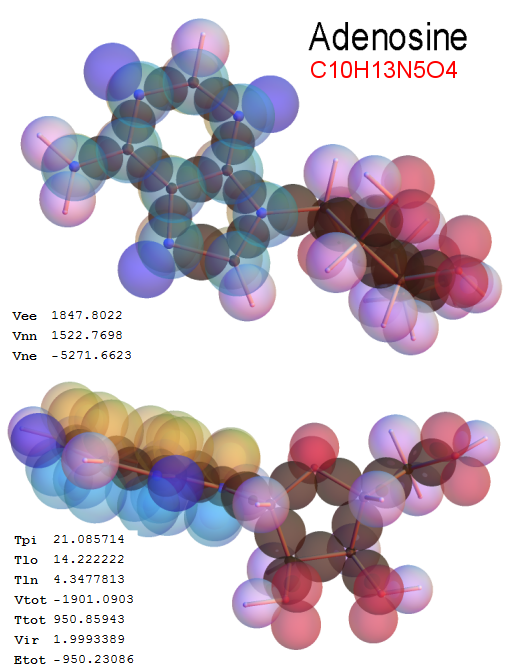
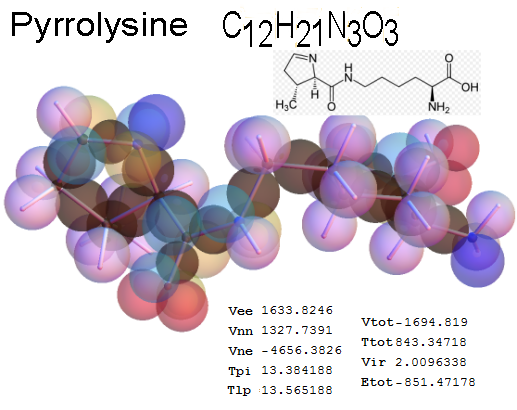
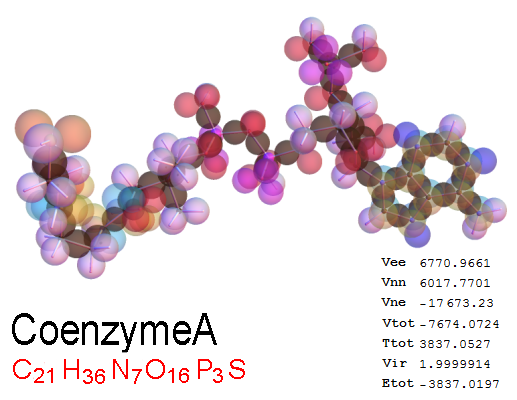
Now, we do this a bit more precisely, using the same structure repositories, theoreticians get their input from. The Kimball core radii of C, N, O, P, S, Cl, and other atoms, do not vary much within most of organic chemistry. The same is true for the positions of the protons in X-H clouds, if the differences | between C-H, N-H, O-H a.o. are applied. Since the groundstate structure is an energy minimum and the observed structure (hopefully) not much different, we do not need to go through a minimization of the total energy functional. We just insert a Kimball two electron cloud (for even molecules) between two cores, fixed at the vertices of the experimental structure and thus determine the cloud radii. Attach H-atom clouds over the protons, touching the bonding core and using the known excentricity of the proton. Add π electrons and lone pairs as required (this is non trivial!), using radii and structures determined with small gauge molecules (as fragments). This fixes all the radii, and hence the total kinetic zero point energy of the molecule. Vtot = Vee+Vne+Vnn: Vnn is simply summed from the experimental structure and the charge of the nuclei. Both, Vne and Vee, can be determined with the usual Kimball procedures, knowing cloud and nuclear positions. The Virial Theorem requires Vtot = -2*Ekin and Etot = -Ekin for an equilibrium structure, which can be checked.
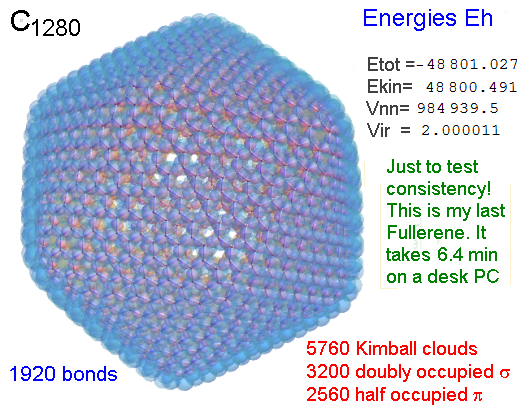
A Mathematica-9 notebook includes the steps described. It allows to obtain the groundstate energetics of arbitrary molecules, given their structures, within seconds or a few minutes, see C1280 below. Computing the terms mentioned produces all energy components for the groundstate and, simultaneously, a check of its consistency, e.g. the Virial Ratio and empirical indices.
|