Chapter 4: Weight Transfer
Any vehicle has a certain weight, in static conditions (no movement), that weight is distributed as explained in chapter 6. Newton's third law, force = mass * acceleration, implies that whenever the vehicle accelerates in any direction, additional forces occur. For example, when your car lands after having taken a jump, its downward velocity decreases rapidly. Basically, it stops falling down quite suddenly. The extra force associated with this equals the mass of the car times its acceleration.
To put this into a numerical example: suppose the car has been falling down for 1 second. Right before it hits the crust, its downward velocity equals G * 1 second = 10 m/s. Suppose the car weighs 1 kilogram = 10 Newton, and its suspension needs 0.1 second to absorb the impact of the landing. The force exerted on the tires is 1kg * 10m/s / 0.1s = 100N = 10kg. So the split second the car lands, it weighs 100 N instead of 10 N.
The point Iím trying to make here is the following: the weight of a vehicle, and hence also its tire loads, varies all the time. Its mass stays constant though. Well actually it doesn't; it varies with speed, but for now let's pretend Mr Einstein has never been born, it doesn't make any significant difference anyway. Unless of course you're so fast you approach the speed of light, in which case there's no valid information on this site :-) Additional forces exist whenever there's acceleration, or in other words, whenever the value or the direction of the velocity changes.
Why is this important, you may ask. Simple: the amount of weight on each tire determines its gripping capabilities, and hence, the handling of the car. In fact, it's safe to say that controlling the weight transfer is the single most important thing in racing, and also what distinguishes good drivers from mediocre ones. Knowing where your car's weight is and keeping your tires right on their limits without suddenly crossing it is what makes you fast.
Because we race in a 3D world, weight transfer can occur in 3 directions. (in a 4D world it'd be too easy to cheat I guess) If there's movement up or down, weight can be added or subtracted. The vertical dimension is a little different from the two horizontal ones, because of gravity. Your car can go from being its normal weight (on a flat road) to being several times as heavy (hitting an uphill section or the face of a bump) to being weightless (flying through the air) to weighing less than normal (on the downside of a bump or elevated piece of track). And don't forget, there's also downforce, which also increases the car's weight. Luckily, in the other two dimensions, the total weight is constant, it can only shift from one side to the other. Like when you're accelerating, weight is shifted from the front wheels onto the rear wheels, but the total remains the same. When you're negotiating a corner it's the same deal, just in another dimension: weight shift from the inside tires onto the outside tires,
a
nd again, the total remains the same. For simplification, let's ignore the first case, and pretend the track is completely flat from now on.
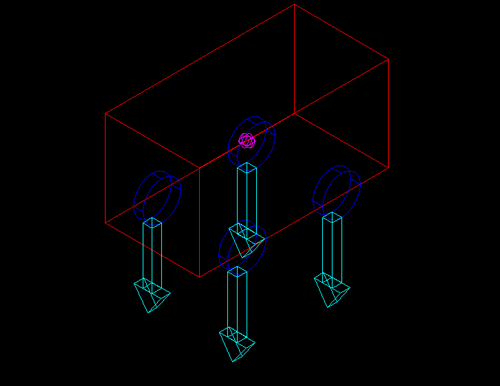
Consider this car: its CG (purple) is located right in the center. It's rolling along at a constant speed (if it's standing still its speed is constantly zero), on a perfectly flat surface, straight ahead, so all tires are loaded equally. If the car's weight is W, the weight on each wheel is W/4.
Note: there's a small inconsistency in the drawings: the cyan colored arrows are to be interpreted as the weight that's on the tires. The inconsistency is the fact that all other forces are drawn as being exerted on the car, and these are drawn as being exerted by the car.
4.1 Lateral weight transfer
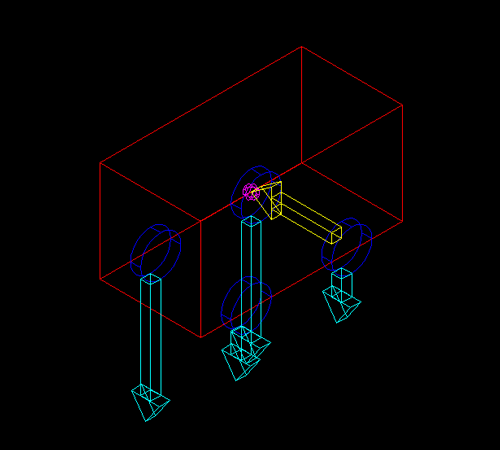
This is the same car, negotiating a turn. It's still travelling at the same, constant speed on a flat surface, only the direction of its speed vector is changing. The radius of the turn is also constant.
First of all, not all forces are drawn, it would have overloaded the picture. On each tire there's a horizontal force, the four of them counteract the yellow one. They're basically the gripping forces of the tires on the road. The weight vector isn't drawn either, it should be acting downwards at the Cg. (purple) the other ones are drawn.
The yellow arrow indicates the centripetal force. It's a result of the inertia of the entire car. It acts in the CG, and is directed away from the center point of the circular path the car is following. This force results in a torque exerted on the car, which has to be counteracted as described in Newton's second law. The counteraction is in the fact that the outside tires are loaded heavier than the inside ones. Because the total weight of the car stays constant, all of the weight that is removed from the inside tires is added to the outside tires. In other words, the weight has shifted, towards the outside of the turn.
The results are important as well as numerous. Unequal loading of the tires usually means that the total amount of grip is reduced, resulting in less cornering power. Also, the torque mentioned before can make the body roll. In this example the car's body won't roll, because it hasn't got any suspension. The body won't roll either if the CG is on the roll axis. The fact if the body rolls or not doesn't influence the amount of transferred weight. (supposing the CG doesn't move around that much as the car rolls) It does however determine where most of the transferred weight is going to go. Sure, in this example it's easy: whatever comes off the left front is going on the right front and whatever comes off the left rear is going onto the right rear. In other words, the car is symmetrical, and it stays that way because it has no suspension. But in a real car it's different: suppose the rear of a real car rolls way more than the front, because the rear RC is very low or the rear springs are very soft. More wei
ght will be transferred onto the right rear tire. Sure, there will also be some weight transferred onto the right front, but it will be less. This makes for an understeering car. And on top of that, there's braking and accelerating, they also transfer weight from front to rear or the other way around. That's why you can usually loosen up an understeering car by braking a little; it transfers weight to the front, where you can use it to provide a little more front traction to steer your car. All things considered, determining how much of the weight is going where isn't easy. Lots of things come into play, like spring rates, anti-roll bar stiffnesses, roll center heights, suspension travel,...
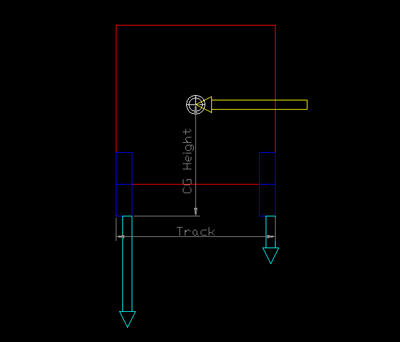
First, let's focus on how much weight is transferred. It's easy to derive that the amount of weight transferred, in essence the difference in weight on the two tires, is equal to the centripetal force (yellow) multiplied by the height of the CG divided by the track of the car. The centripetal force is equal to the car's lateral acceleration, expressed in Gs, times its total weight. The lateral acceleration is equal to the speed of the car squared divided by the radius of the turn.
From this we can conclude that the amount of transferred weight is proportional to the height of the CG, and inversely proportional to the track of the car. This is why most race cars are built as low as possible and as wide as the regulations allow; it minimizes weight transfer, which in turn prevents a decrease in overall traction. It is also proportional to the car's static weight, another reason why race cars have to be as light as possible, again to minimize weight transfer. The amount of weight transferred is also dependant on factors that don't refer to the car itself, like its speed, and the radius of the circle which approximates the path it is following. The fact that the amount of weight transferred is proportional to the radius of the turn is one of the reasons why a large, smooth radius is the fastest line when cornering: it minimizes weight transfer, so it maximises overall grip and cornering power.
4.2 Longitudinal Weight Transfer

It's basically the same deal as lateral weight transfer, but it works in another dimension. This time the car is running straight ahead, (white arrow) on a flat surface, but it's accelerating. In other words, its speed is increasing, or in the words previously used, its speed vector is increasing in size but its direction remains the same.
Again some forces aren't shown: the forces that propel the car for instance. They act in the contact patches of the driven wheels and are in the same direction as the white arrow. The car's weight also isn't drawn.
As always when an object is subjected to acceleration, there's an inertia force, acting in the CG (drawn in yellow) This results in a torque, which is compensated by a shifting of the weight from the front tires onto the rear tires. Whatever weight comes off the front tires is added at the rear tires, and as long as the acceleration happens in a straight line, it happens symmetrically.
Having a little more weight on the back tires can be a good thing for a rear wheel drive car that's accelerating in a straight line, but because of the reduced weight at the front, it will understeer horribly. The same principles apply as with lateral weight transfer: because the tires are unequally loaded, the total amount of grip available is reduced. That's why the absolute quickest way around a corner is without braking or accelerating. Needless to say you need a well balanced car for that, one that doesn't under - or oversteer. Another thing that applies is that the weight transfer is independent of the vehicle's pitch angle. The car will probably dive when braking and squat while accelerating, but the amount of weight is unaffected by this. Unless of course the height of the CG changes dramatically. This can happen if the car has a lot of negative suspension travel. Imagine that the front lifts off quite high, and the rear doesn't squat very much. The CG will rise a little, which in turn promotes
more weight transfer. This is how wheelies begin, the CG rises, which makes for more weight transfer, which makes for more rear traction which can cause the front to rise even more... it's kind of like an avalanche effect.
The formula for the amount of weight transferred is very similar to the previous one. Now it's the inertia force times the CG height, divided by the wheelbase. (instead of track) the inertia force is equal to forward or rearward acceleration times the car's mass. So a low CG and a longer wheelbase produce less longitudinal weight transfer. And as always, the transferred weight is proportional to the acceleration.
As explained earlier, race cars have to be low and wide, so from the previous you'd expect that they'd also have to be as long as possible. This is not always the case. Rear-wheel drive cars, for example, can use some more weight on their rear tires as they accelerate, to keep them from spinning out. A little understeer under acceleration allows you to really put the power down without having to worry about wheelspin.
But that's not the only reason; cars with long wheelbases tend to handle a little sluggish in tight, low-speed corners, they're not nimble enough. So, in general, a long wheelbase is better for big, smooth, high-speed tracks, and a short wheelbase is better for tight, twisty tracks.






