Decimalización del dinero.

ENIENDO, como suele tener el ser humano, cinco dedos en cada una de sus dos manos, lo que hace un total de diez, de los que desde tiempo inmemorial se vale para contar, es lógico que nuestro sistema numérico tenga al número diez por base desde hace muchísimos siglos, aunque hay excepciones, como el ingeniosísimo sistema vigesimal maya, que sólo usaba tres signos básicos para representar los números. La decimalización de los sistemas monetarios es, sin embargo, muy reciente, sobre todo en lo que llamaremos, a falta de mejor denominación, ‘decimalización física’, por contraposición a la meramente contable. Esta última, consistente en dividir la unidad en diez (o más frecuentemente, cien) fracciones para facilitar el cómputo, no surgió hasta el siglo XVIII. Hasta entonces venían usándose sistemas tradicionales de base 8, o que se comportaban como un sistema octal, en el que el valor de una moneda a la siguiente se multiplicaba por dos, o también, como en el caso de Inglaterra, un sistema que tenía una base distinta para sus distintos tramos: 12 para el tramo de los peniques, 20 para el de los chelines, etc., lo que permitía prescindir del redondeo en muchísimas ocasiones, al ser el sistema divisible por los cuatro submúltiplos de 12, por el mismo número 12, y también por el 20 y sus submúltiplos. Es decir, el sistema era divisible por 1, 2, 3, 4, 5, 6, 10. Por el contrario, el diez sólo tiene tres submúltiplos: 1, 2 y 5. El sistema de base 8, disfrazado o no de sistema decimal, tiene la ventaja de que se puede sustituir una moneda por dos del valor inmediatamente inferior.

Historia de la decimalización

Es en el siglo XVIII cuando surge con fuerza la decimalización en todos los ámbitos: metrología, aritmética, geometría, dinero, etc, con el ánimo de facilitar y promover el comercio y la industria. Surgió el sistema métrico decimal, el mayor éxito de esta campaña que inició la Revolución Francesa. Hoy es de uso prácticamente universal, pero otras propuestas no tuvieron tanto éxito: incluso se llegó a proponer un cuadrante de círculo de 100 gradientes, en vez de los tradicionales 90 grados. Esto permitiría tomar como base de las medidas lineales la diezmilésima de cuadrante de meridiano, que es igual a 1 km. Quienes por entonces dominaban los mares (Gran Bretaña) decidieron seguir usando el viejo cuadrante de 90 grados, divididos cada uno en 60 minutos, que se tomaban como base para medir distancias y velocidades: 1 minuto de meridiano = 1 milla náutica. El sistema sigue en uso hasta hoy en la navegación marítima y aérea y, aunque el kilómetro ganó la batalla terrestre en casi todo el mundo, el cuadrante de 90 grados es universal. En lo que se refiere al dinero, la decimalización, que nació también con la Revolución Francesa, fue adoptada de forma entusiasta en Estados Unidos, país que ganó su independencia por aquellas fechas, y que creó una unidad de cuenta, el dólar, dividida en 100 centavos. El dólar estaba inspirado en el real de a ocho español, principal medio de cambio en toda América, al que debe su composición e incluso, según la teoría más extendida, también el símbolo tradicional ($), que sería una adaptación de las columnas de Hércules y la cinta con la expresión latina ‘Plus Ultra’ enlazada entre ellas. En cualquier caso, la nueva moneda convivió con las monedas españolas y otras hasta mediados de siglo XIX. La antigua metrópoli, Gran Bretaña, no renunció a su característico sistema tradicional, que mantuvo hasta 1971, año en que la incorporación al Mercado Común Europeo obligó a la decimalización, tanto contable como física. Fue también entonces cuando se empezó a acuñar las monedas (las de 50 nuevos peniques) en forma de heptágono de anchura constante, adaptación de la tradición de monedas de forma poligonal a los nuevos tiempos de las máquinas expendedoras y tragaperras. Es de señalar que Gran Bretaña, que en su territorio metropolitano se aferró a su sistema tradicional con uñas y dientes, es quien más ha contribuido, mediante las acuñaciones para sus colonias, a la difusión de la decimalización, en su doble aspecto contable y físico, por casi todas las partes del mundo que estuvieron bajo su dominio.

‘Decimalización contable’ y ‘decimalización física’.

Ya hemos explicado que es la decimalización contable pero, ¿a qué llamamos decimalización física? A la utilización de valores nominales coherentes con un sistema de base diez. Esto se consigue haciendo que todos y cada uno de los valores nominales de un sistema sean producto de multiplicar un submúltiplo de diez (1, 2 y 5) por una potencia de diez (1, 10, 100, 1000, etc.), según vemos en el siguiente cuadro:

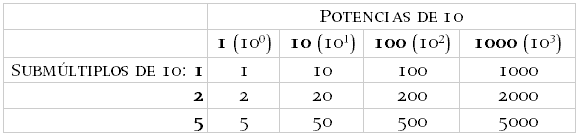
De esta manera se consigue un sistema coherente, fácil de usar, y que puede extenderse sin límites hacia arriba o hacia abajo manteniendo la facilidad de cálculo, principal ventaja de la decimalización. Se comprende, a la vista de esto, que valores nominales como 25, ¼, e incluso aberraciones como valores nominales mayores que 1 y no enteros, como la moneda española de 2,50 pesetas, simplemente no tienen cabida en un auténtico sistema decimal y son pervivencias de los antiguos sistemas octales tradicionales. Con la llegada del euro, son varios los países europeos que tienen por vez primera un verdadero sistema decimal, entre ellos España.

Y ¿el 3?

En los primeros días de circulación del euro ya había, al parecer, falsificaciones. Apenas llevaba la flamante divisa dos semanas en circulación cuando se divulgó la noticia de que en Finlandia había sido detenido un hombre por intentar pagar los servicios del taxi con un billete falso. Pero esto no era la noticia: la noticia era que el billete falso tenía un valor nominal de 300 euros. Como no existe el billete de ese valor, el personaje fue de inmediato detenido. La idea de hacer un billete falso de 300 euros es una estupidez, pero el hacerlo auténtico quizá no lo fuera tanto. Ya hemos visto que los submúltiplos de 10 son 1, 2 y 5, y que alguno de ellos es uno de los factores que da lugar a todos y cada uno de los valores del sistema. Esto supone que en cada tramo se pasa del valor originado por el 2 al originado por el 5, que es 2,5 veces mayor. Por ello, hacen falta al menos 3 monedas de valor inferior para sustituir al 5, 50, 500, 5000, etc. Una moneda de 5 sólo podría sustituirse por dos de 2 y una de 1. La secuencia de Fibonacci (1,1,2,3,5,8,13,21,etc.), en la que cada elemento es la suma de los dos anteriores, nos da la solución: bastaría incluir el número 3 entre los submúltiplos de 10 para, al multiplicar por las potencias de diez, generar los valores 3, 30, 300, 3000, etc, lo que permite que en todo el sistema un valor sea sustituible por dos monedas de valor inferior, ya que 2 + 3 = 5. El 3 no es un submúltiplo de 10, pero es una solución menos estridente y más 'decimal' que las monedas de 2,50 ó 25, ya que la utilización del sistema aquí propuesto da siempre como resultado un número entero y, salvo el 3, múltiplo de 10. El resultado es, pues, un sistema decimal y algo más. Este sistema ya tiene antecedentes en la Rusia de épocas zarista y soviética, donde fue muy utilizado, así como en los Estados Unidos de América, donde se acuñaron monedas de 3 centavos entre 1851 y 1889, si bien es cierto que no se trataba de sistemas enteramente decimales, puesto que había otros valores absolutamente incompatibles con lo que aquí se expone.

Lea esto