Contributionsto module-theoretic classification of musical motifs
Text-only version of this page

Note: Non-reversible transformations

I already mentioned that our definition of isomorphy does not include all motif variations that are used in music. Among those are also all affine transformations that are non-invertible; important examples are pitch and time expansion. If we want, wecan take these into account as well; the result will be a classification with a rather different structure. The main difference between isomorphy and the relations between motifs connected through a non-invertible transformation is that the latter is not symmetric: If there is a transformation mapping the motif m1 to m2, there may be no way back. So, whereas "isomorphy" defines a real equivalence relation, the relation involving non-invertible transformation is of a hierarchical nature. It can be visualized as a directed graph (a so-called Hasse diagram). We will give an example later.

Basic properties of ZxZ and Z12 x Zn

ZxZ and Z12 x Zn are Z-Modules. (A module is much like a vector space but based on the mathematical strucuture of a ring instead on a field.) We begin by stating some of their basic properties which are in many aspects similar to those of the Euclidean plane.

From now on, we will mainly look at the special case (Z12)^2and the measure-independent case Z^2. In statements valid for both we will write R^2 where R stands for "Ring" (since Z and Z12 are both rings). (Z12)^2 is also a Z12-module.

There are basically 2 types of affine transformations:translations (every point is moved one constant vector) and linear transformations which have the origin (0,0) as a fixpoint. Every affine transformation can be written as the concatenation of a translation and a linear transformation.

Affine transformations leaving (0,0) fix are nothing but Z-module-homomorphisms from R^2 to itself; they can be written in the usual way as matrices:

The group of invertible linear transformations of R^2 (=the group of module-automorphisms of R^2) is generally denoted withGL(2,R) (the general linear group on R^2). The corresponding matrices have invertible determinants in R.

Here is the point where a first important difference between R^2 and the Euclidean plane shows up: in the latter, every matrix with non-vanishing determinant is invertible. But since we work with a ring, this is not the case. In Z, there are only 2 invertible determinants: 1 and -1. In Z12, the possibilities are1, 5, 7 and 11 (7 being equal to -5 and 11 being equal to -1).The subgroup of transformations whose determinant is 1 is denoted with SL(2,R) (the special linear group on R^2).

Lemma 1:

1. GL(2,Z) is generated by the following transformations:
   (time inversion)
   (transvections)
   
2. GL(2,Z12) is generated by:
   where a is invertible in Z12
   (transvections)

Sketch of proof:

Let m be the matrix of an arbitrary transformation in GL(2,R).Let d be the determinant of the matrix. Then multiplying m with the matrix

will result in a matrix with determinant 1, hence belonging to a transformation in SL(2,R).

Let now m2 be the matrix of a transformation in SL(2,R). Multiplication with one of the transvections from left or from right can have one of the following effects: adding one row to another row or a column to another column, subtracting a row from another row or a column from another column. The basic idea is to use a sequence of such row/column operations until the transformed matrix is the unit matrix; the decomposition is then given by the inverses of the involved transvections.

I skip this here (if I were a nasty professor, I could say: I leave this as an exercise).

Additional notes concerning generators of GL(2,R)

1. In Z12, the transvection is equal to .
2. Musical interpretation of the transvection : It transforms a chord into an arpeggio based on the chord tones.

Classification of motifs with 2 elements

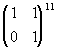We are now ready for the classification of motifs consisting of 2 tones.

THEOREM:

Let R be Z or Z12. Then, any 2-element motif in R^2 isisomorphic to a motif of the form { (0,0), (n,0) }.

Proof:

With pitch and time shift, any motif can be brought into the form { (0,0), (x,y) }. From now on we consider only transformations in GL(2,R), so we can forget about the point(0,0).

If y is 0, we are finished. If x is 0, we use the parameter switch transformation and are finished.

Assume now that both x and y are > 0 and that x>y (the other cases are handled in exactly the same way but with another transvection). Then the transvection

transforms (x,y) into (x-y,y), x-y still >=0.

We repeat this transvection until the x coordinate is smaller than y but still non-negative. If it is 0, we are finished (see above). If it is >0, we do the same with the transvection

which decreases the y coordinate by the value of the x coordinate until the y coordinate is smaller than the x coordinate. After finitely many steps, one of the coordinates is necessarily 0.

Now, what is the value of the last remaining non-vanishing parameter? If we look at the calculation steps we executed we see that they describe nothing but the Euclidean algorithm to get the greatest common denominator of 2 numbers! Hence: