Atoms with non overlapping spherical clouds: to be prepared


  Li to Ne, computed with σ = 0.3 in 1s2-core and 2-el clouds

  1. Li1_Ne1 computed with Mathemathica, shown as html: from Li to Ne, for C to Ne in simplified tetrahedral structure and equal size singly and doubly occupied clouds, then for N to F also with different radii
  2. Li2_Na2 computed with Mathemathica, shown as html: from Be+ to Ne+, O+ to Ne+ also in correct (C3v, C2v, C3v resp.) structure with different single and double clouds
  3. neutral Li to Ne all numerical values to help adepts of qualitative "art", "styrofoam" or "cork"-Kimball models to (at least) demonstrate correct relative sizes (there is not one of them in the literature which shows any concern for similitude with the correct Kimball model!)
  4. Li+ to Ne+ Ionizationpotentials and "Aufbau" Principle. The blue experimental values - see figure below - show the well known filling order s1,s2,px1,py1,pz1,px2,py2,pz2 from Li to Ne, manifesting the 2s and 2p subshelle with 2 and 6 electron places, resp.. s-electrons are more stable than p-electrons and the pairing of two electrons in one orbital costs energy, hence the fifth electron in N causes a dip in the IP (sorry, this is basic chemistry stuff!). The pink values pertain to the Kimball IP's and, therefore, show filling order 1,1,1,1,2,2,2,2 as suggested by the Lewis dots and dashes in accord with the known number of electron pair bonds being available. The three green values belong to O+ to Ne+, isoelectronic with N to F and with different radii for singly and doubly occupied clouds. Their IP's are a bit nearer to experiment, since the filled clouds are larger and the 3,4,5 occupation of the sp-shell produces non tetrahedral Lewis-Kimball atoms.
In general the Kimball non overlapping model does not do badly with the total energies, a bit less with the ionization potentials. The ionization process of an atom connects two spherically symmetric eigenstates.
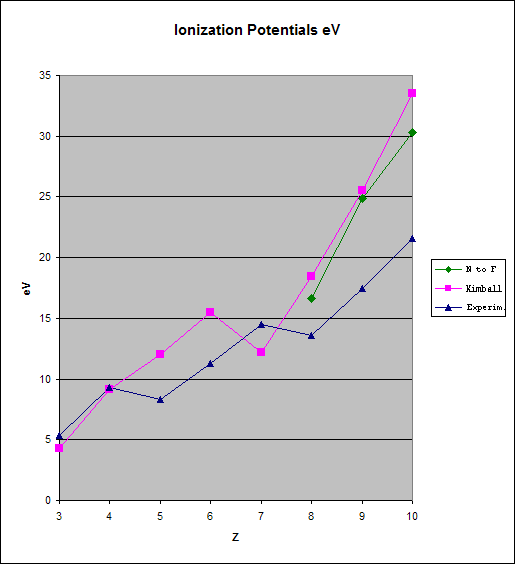
For these the Aufbauprinciple requests and explains the blue IP sequence. For the pink Kimball values this is definitely incorrect. Ok. But, what do you try to understand? Lewis' and Kimballs chemical atoms are meant to be used in a chemical context, which is never spherically symmetric. For this the spherical eigenstates of an isolated atom are inadequate and don't apply. The four-"valent" Lewis/Kimball C-atom has been replaced by the physicists spherical 2s2p2 atom. This caused a problem for every chemistry teacher: Why does the C-atom with two half filled orbitals form four and not only two electron pair bonds? The problem does not exist if the cart is not put before the horse. Symmetry comes before the eigenstates because the symmetry of the external perturbing field creates the correct eigenstates and not the other way round: If the isolated, spherical C-atom with 2s2p2 3P senses ligands		 nearing, the valence electron shell spontaneously responds. If it's one ligand only, a cylindrical deformation happens (e.g. CO formation), if there are four equivalent ligands, a tetrahedral field may distort the shell. This is a completely new situation with a broken-up relation to the original spherical environment. The C-atom is now forming symmetry-adapted incipient molecular orbitals with, perhaps, Td symmetry. s2p2 splits into a11+t23 orbitals, decoupling the pair of s2, with s going down in energy into a1 and p going up into t2 orbitals. This does not cost energy since the energy loss for s is exactly equal to the sum of the gains of the p electrons. If the shell is half filled - C reacts - or filled - molecule formed - we have spherical symmetry again. But it is NOT sp3 but a1+t23. The energy gap between the two is clearly observable by photoelectron spectroscopy and two different ionization potentials (Mulliken 1935), wheras the (accidentally) degenerate s and p orbitals (spherical symmetry) do not show an energy difference. The usual cheap jargon "sp3 hybrid orbitals" is wrong! It makes believe, that a structure is caused by clever combination of orbitals instead of teaching, that the symmetry of the external field creates an appropriate electron distribution. The innocent student gets deluded with a kind of truth, he is not able to understand. If a knowledgeable scientist talks about "sp3" he probably means this as a shortcut label for the deeper truth sketched above. But, sp3 does not explain anything to an untrained mind and destroys scientific education with esoterics. Of course, a beginner does not understand a1t23 as well. So, why not just state: When a C-atom is exposed to a tetrahedral ligandfield it deforms its spherical shape observably into a tetrahedron deploying four chemically (not spectroscopically!) equivalent bonds, period? Kimballs four equivalent single spheres or Lewis' four equivalent dots of the C atom are meant to represent this experience, and not C's ionization potential. Variations of this story can now be developed for other symmetries, no symmetries, and any atom.

However, I'm not as stubborn as all this: If a colleague talks about "sp" or "sp2" ... I assume that he means "cylindrical, i.e. digonal" or "trigonal" symmetry, but please, not in the inverted sense. I am less happy if chemists use e.g. the label sp3 for any four-bonded carbon (or other atom), even when the structure is far from tetrahedral, say CH2F(OH). Sorry, but this misuse (in textbooks and even research literature) should not be tolerated by a responsible reviewer! And HAB: There is room for Bent's rule. The nearer to a nucleus a phenomenon manifests itself the weaker is its response to the perturbation of a deformed valence shell. The dramatic exponential increase of electronic density towards the nuclear cusps makes them centers of spherical harmony and (nearly) true deployers of spherical functions like s,p,d ..., - hence Bent's rule and other s-p(-d extended Bent!) effects. It is a subtle art to deal in second order effects. Often, not even their sign is certain.

    Kimball Atoms from Na to K