
| This is the second comment to the Kimball-Loebl paper from 1959. It pertains to the main issue: "What is the chemical bond between a transition metal ion and its ligands?" and stresses the fact that chemical bonding is an electrostatic effect. The paper is based on a talk Kimball had given at a symposium "Advances in Chelate Chemistry", NY, April 29-30,1955 (published 1959). The historical environment has been the episode named "Renaissance of Inorganic Chemistry". Not long before, chemists had rediscovered Hans Bethe's Crystalfield theory from 1929 (and J.H. van Vleck 1932) and at about Kimball's talk the Ligandfield theory was in full development. These theories had given, for the first time, a successful explanation for various colors of transition metal complexes and their dependence on ionic charge and nature of ligands. Many chemical properties, hitherto not understood, were getting simple explanations. Kimball's talk did not adress any | of this (he probably had not read the newer literature and was
already deep in his new life: Operations Research). It must have been an
anticlimax for an audience eager to learn more about the current exciting
happenings.- However, this is still a very valuable paper for its clarification of the role of quantum chemistry for explaining chemical bonding and other chemical phenomena. It stresses the fact, that chemical bonding is an electrostatic effect, to be described in the framework of quantum mechanics with the electronic zero point kinetic energy as spring and the electrostatic interaction as bolt = "Stell-schraube", preventing molecular electrostatic collapse and, of course, Pauli's Principle telling you, why a baby is hurting when he bumps his head into a solid wall. *) In what follows the type of calculations suggested but not actually presented in the paper, will be done and critically discussed: |
|
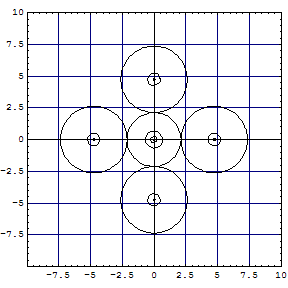
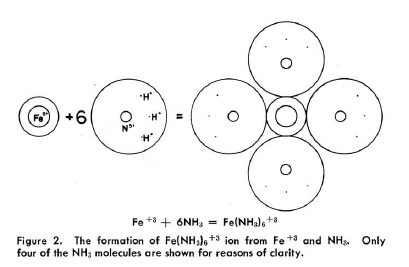
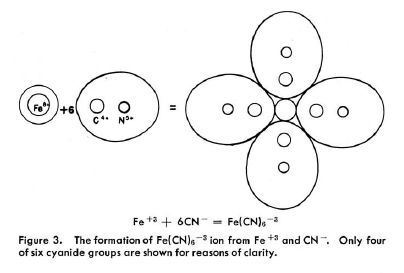
In Kimballs' spirit: "The difference between the dipole ligand NH3 which only
superficially attaches itself to the central ion with anionic and possibly σ-donating
ligand CN-, going deeply into the electronic structure of Fe3+ is
clearly shown by the extension of the central sphere, representing the electronic environment
of the Fe-ion". The problem is, that |
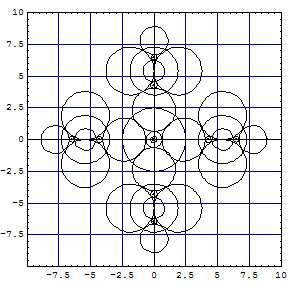
| A computation of the hexachloro complex gives the following cut of Kimball
spheres in one of the three σh planes: |
The partial projections of the Kimball model calculation of
|
 |
 |
 |
| The left plot is not too different from Kimballs' sketch. The middle and right have indeed a much smaller Fe core. The FeII complex has been modelled such that the Fe-C bonds go down in to touch the Ar-core of FeII, which left the nonbonding t2g6 orbitals on top in a superimposed shell. This gives results similar to a computation with Gamess and model chemistry |
|
Details for the Hexacyano-ferrate(III)
Kimball computation:
FeCN6III4a
Radius R1 : 0.0575706 R1 = 0.0575706
Radius S2 : 0.2851409 R2 = 0.1796275
Radius S3 : 0.6986901 R3 = 0.4401472
Radius S4 : 1.4268294 R4 = 0.7852145
d C-N [┼]: 1.1518469 R5 = 0.2596144
d Fe-C [┼]: 2.2734710 R6 = 0.2237458
Etot(R) : -1808.25436 R7 = 1.3048974
Vne(R) : -5576.63530 R8 = 0.8466577
Vee(R) : 1429.85433 R9 = 1.9022481
Vnn(R) : 530.27227 R10 = 1.0956922
Virialtheorem : Epot/Ekin = -2.000000000
Z = 26.0 Z1 = 6.0 Z2 = 7.0 vars = 11
|
Details for the Hexacyano-ferrate(II)
Kimball computation:
S4 is the radius of the t2g shell:
FeCN6II8
Radius R1 : 0.0575026 R1 = 0.0575026
Radius S2 : 0.2829547 R2 = 0.1782503
Radius S3 : 0.6419421 R3 = 0.4043982
Radius S4 : 2.4990094 R4 = 1.3752579
d C-N [┼]: 1.1519820 R5 = 0.2603177
d Fe-C [┼]: 2.2729893 R6 = 0.2237594
Etot(R) : -1810.43716 R7 = 1.6965343
Vne(R) : -5616.43574 R8 = 0.8464270
Vee(R) : 1465.19668 R9 = 1.8900762
Vnn(R) : 530.36474 R10 = 1.1024983
Virialtheorem : Epot/Ekin = -2.000000000
Z = 26.0 Z1 = 6.0 Z2 = 7.0 vars = 10
|
| *) It is uncanny, how the development of science may exhibit synchronicity: Both Crystal Field and Ligandfield theories were identified soon after their inception as simplified aspects of the already existing much more elaborate Molecular Orbital theory, which at the time had not yet been applied to (or was not recognized in) the realm of inorganic coordination chemistry (dominated by Valence Bond arguments of Pauling). Synchronously, various restricted theories or models populated the horizon of organic chemists: HŘckel MO, PPP, CNDO and various other schemes of neglecting this and that in the Hamiltonian. As soon as MO theory had developed enough power, they all collapsed as well. One rather sad aspect was e.g. the only marginal reception of the didactical masterpiece: "The HMO-Model and its Application" by E. Heilbronner & H. Bock (1968/76, Verlag Chemie, GmbH, Weinheim/Wiley, Interscience publications), which appeared a couple of years too late.- Nowadays, it is still the pearl of many inorganic chemists curriculum and textbooks to relive the days of the "renaissance" with celebrating the Ligandfield splittings of various high symmetry complexes. Usually it is not told that this all can now be had by the elaborate tools of MO-theory in much better quality. Indeed, it has been one of my jokes, some 30 years ago, to show students a HMO treatment of tetrahedral and octahedral threedimensional(!) | complexes, giving e.g. the splittings of tetrahedral functions into a1-t2 or octahedral into a1g-tg2-eg. You can test this by going to Chemsoft's Archive/Chemical Education and downloading chemedu.zip. After unpacking you'll discover HMO.exe in CHEMUNT/ATOM_MOL. Run it in DOSbox (32 bit!) and construct automatically the HŘckelmatrix of an octahedron by describing 12 octahedral edge connections as 1-2-3-4-5-6-1,1-3,1-5,2-4,2-6,3-5,4-6. HMO now produces the eigenvalues and eigenfunctions (their pictures, it's not benzene!). The resulting level scheme with a1g, t2g (or t1u), empty eg, is what you find in modern textbooks of inorganic chemistry. And then it should make "click" in your head: This is a simple manifestation of diagonalizing a 6x6 matrix with correct elements representing the symmetry of the problem! We need not even specify what makes up the representations (Heilbronner often talked about HMO as a Zen (buddhistic) art). If the bases are even functions, e.g. (x2+y2+z2),s, d,... orbitals, or cosines, we have t2g and eg, for odd functions like (x,y,z),p orbitals or sines, t1u, eu irreps. And, please, forget all the conundrum with Pauling's hybridization - it does not explain anything. It is symmetry that counts. Orbitals are just one way to select bases for its representations. |