Chapter 6: Weight distribution
Weight distribution is very important; not only does it affect the static weight on the different tires, it also affects how the weight shifts in dynamic conditions.
The easiest way to judge weight distribution is to determine the car's Center of Gravity (CG). This is a point in space where the mass of the entire car is accounted for. Because of its location, it can be used to simplify the effects of inertia forces. In reality, every little bit of mass is subjected to inertia, but it's much easier to make use of an equivalent condition: assume all the mass of the object is concentrated in its center point, i.e. it's CG. So instead of having to figure out how every part of a 1.5kg car reacts to a certain force, we only have to figure out how a weightless car with a 1.5kg dot in it's center(the CG) reacts to it. The latter is much easier: the force only works in the CG, and not in the rest of the car.
Of course, this only works when the CG is determined correctly. One method to achieve this is explained here. I think that's a lot of work, and it might not be accurate, so I propose a different method. It's based on the fact that when an object is statically balanced, its CG is right above the point where it's supported. By applying this in three different planes, you can determine an object's CG. Here's an example.
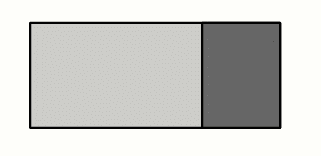
Here we have an object with a heavy part (dark) and a lighter part (bright) we'd like to determine the CG of. Since the right part is heavier the CG will probably be located somewhere at the right.
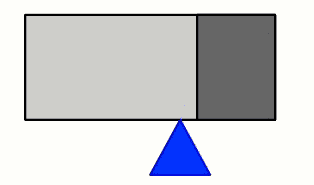
We try to balance it on a sharp edge, and this is the position in which the object stays put. So we know the CG is somewhere right above the point where the object is supported.
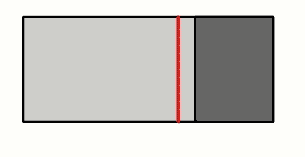
The red line contains all the points above the point where the object was being supported, so the CG has to be located somewhere on the red line.
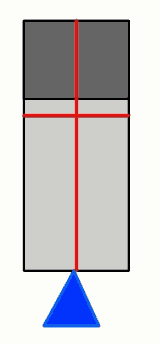
We can follow the same procedure, but in a different dimension. Again, we can draw a red line on which the CG is located.
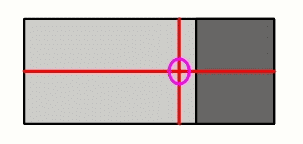
Because this is a 2D example, trying to balance the object 2 times is sufficient to determine it's CG(circled in purple). For a car, which has 3 dimensions, you'll need to do it 3 times. It might impose some practical problems, but this is where you'll have to use your imagination.
Now that we know where the car's CG is located, we can easily calculate the amount of weight on the tires, and the weight distribution.
First, let's have a look at the front-to-rear weight distribution:
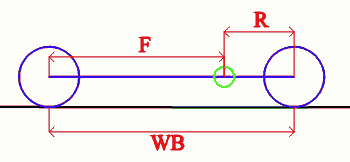
The wheelbase is the distance between the front and rear axle, F is the distance between the CG (green) and the front axle, R is the distance between the CG and the rear axle.
Weight on the front axle = weight of the car*(R/WB)
Weight on the rear axle = weight of the car*(F/WB)
Or, in percentages:
Front weight percentage = (R/WB)*100%
Rear weight percentage = (F/WB)*100%
Obviously, this will have its effects on handling: more weight on a tire means more grip. So if the CG is located further towards the rear, the car will have a lot of rear traction, which is nice to have if acceleration is important. If the CG is located further towards the front, the car will have a lot of steering, but it might lack rear traction, which increases the risk of spinning out.
In some cases, lateral weight distribution is a major concern, aspecially in so-called LTO(left turn only) cars, who race on oval tracks. It's basically the same deal:
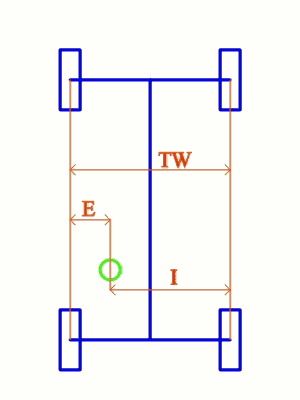
TW is the treadwith, the distance between the centers of the tires at the axle, E is the distance between the CG(green) and the centerline of the left side tires, I us the distance between the CG and the centerline of the right side tires. If the front and rear axles aren't equally wide, E and I have to be measured at the CG.
Weight on left side = (I/TW)*weight of the car
Weight on right side = (E/TW)*weight of the car
Or, in percentages: left side weight percentage = (I/TW)*100%
Right side weight percentage = (E/TW)*100%
Note that if you need to know the amount of weight on one tire, you need to multiply the weight of the car by 2 factors, one of the lateral balance, and one of the longitudinal balance, for example:
Weight on left front tire = Weight of the car*(I/TW)*(R/WB)
Weight on right front tire = Weight of the car*(E/TW)*(R/WB)
Weight on left rear tire = Weight of the car*(I/TW)*(F/WB)
Weight on right rear tire = Weight of the car*(E/TW)*(F/WB)
Note that this is only true when the car isn't tweaked; spring preload should be the same on the left and right hand side.
Again, having the CG away from the center of the car has consequences for the car's handling: having it toward the left improves the car's ability to turn left, but it might make it very difficult to drive the car in a straight line, aspecially under acceleration.
The height of the CG is also very important: it determines the car's roll characteristics and weight transfer. More about this in chapter 2.
Sadly enough, that isn't all there is to it; inertia has been left out, rotational inertia to be more precise. Here's an example:
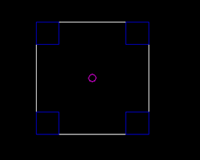
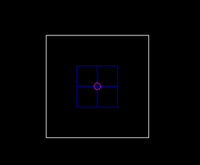
These drawings represent two cars, the first one on the left has all the heavy stuff (blue) located at its ends, far removed from the CG (purple). The second one on the right has all the heavy stuff lined up right in the middle, very close to the CG. Both cars weigh just as heavy, and their CGs are in exactly the same place.
So both cars will transfer the same amount of weight while braking or cornering, and their roll angles will also be identical. Yet they won't handle the same, because their rotational moment of inertia is different. The first car will react slowly, turn in a little sluggishly and it will generally be more reluctant to change direction. Some might say it is slow, others might find it very stable, it's the same thing. The second car will feel like the opposite: it will change direction very quickly, and it will feel very nimble, and thus also unstable.
So, rotational moment of inertia doesn't change how far the car's chassis moves, it changes how fast it does so. It's kind of like swinging a baseball bat with a big, heavy tip: you'll need a lot of effort to get it going, and once you get it going, there's not much you can do to alter its course.
The rotational moment of inertia can be calculated too: the rotational moment of inertia of a body around an axis is the sum of all the elementary masses of the body multiplied by their distance to that axis squared. For simple-looking bodies like cylinders, cubes and cones and such, you can do this by hand, but for real-life applications you'll need a sophisticated CAD program.
Note that it's also important around which axis you're calculating the rotational moment of inertia. Consider the following example:
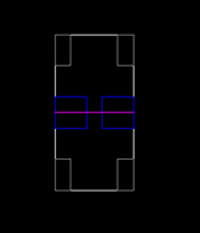
These drawings represent identical cars, except for the fact that they have their weight distributed differently: the first one has its heavy components (blue) lined up along its lateral axis (purple), and the second one has its heavy stuff lined up along its longitudinal axis.
Consider the first car. If we calculate the rotational moment of inertia around its lateral axis, we have to multiply all of the masses with their distance to the axis squared. In this case, we have to multiply most of the mass with a very small distance squared, resulting in a very small value. On the other hand, if we calculate its rotational moment of inertia around its longitudinal axis (not drawn), we have to multiply most of the mass with a very large distance squared, resulting in a large value. So, the first car has a very large moment of inertia around its longitudinal axis, and a very small one around its lateral axis. In other words, this car will react very slowly while cornering; it will move from side to side (roll) very slowly. But, it will move from front to rear (pitch) very easily, this might be beneficial for quick braking, but it will make the car bounce back and forth in bumps, making it very unstable.
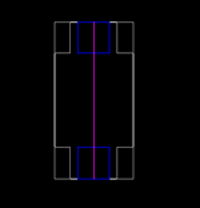
For the second car, the opposite is true: it has a large value for its rotational moment of inertia around its lateral axis (not drawn) and a very small one around the longitudinal axis. This means that the car will roll quickly, and be very responsive in turns, but it will be very stable front to rear. This helps stabilize the car in bumps while maintaining good cornering abilities.
Maybe now you can understand the hype about mid-mounted motors in full-scale cars: the motor is by far the heaviest item, so by positioning it centrally, the car's rotational moment of inertia is reduced, making for a more nimble handling car.













