
Contributions to module-theoretic classification of musical motifs
| Index Previous Next |
Classification, part 4 |
After this theoretical chapter, we come back to the classifications of motifs in (Z12)^2.
The motifs with 3 elements finished, our next goal is the classification of the motifs with 4 elements - an important goal since there, for the first time, not all motifs will be connected via non-invertible affine transformations so this will be the first really "non-trivial" classification. (It is also the first one for which the complete agorithmical solution was not known when I started - we are approaching one of the goals of this work.)
We will first apply the invariants we found so far. Then we present another invariant (a kind of refinement of the subset classification) and apply it. The results in this chapter were mainly achieved with computer assistance, based on a complete - but still untested - list of representants for the classes of 4-elements motifs in (Z12)^2 by E. Köhler ([3]).
We start exactly the same way as we did for the motifs with 3 elements. Computing the volume (the generalized definition) and the isomorphy classes of all 3-element subclasses (computed like described), we get a subdivision of 4-element motifs into "classes" - and it can be hoped that those invariants will completely determine the isomorphy class of a motif.
I tried this out with the help of computers, and the result was: volume and 3-element subclasses do NOT determine the isomorphy class of every motif with 4 elements - but they do in the majority of cases. More precisely, there are 180 different value combinations for the above invariant system that actually occur, hence we can distinguish 180 "classes" - whereas isomorphy, according to Köhler's list (which we will verify later), defines 216 classes. So the classification via volume and 3-element subclasses can still be valuable for analysis (especially since they are easy computable).
We have seen in the previous chapter that for motifs with 2 elements the "range" invariant boils down to the classification of cyclical subgropups of the underlying module. For arbitrary motifs, we need an isomorphy classification of arbitrary subgroups.
Again I merely state the results, which are basic properties of finite abelian groups and should be found in appropriate textbooks.
As every group is isomorphic to a direct sum of its p-components, every subgroup of it is isomorphic to a direct sum of subgroups of the p-components. This means in the case of (Z12)^2 that we have to determine isomorphy classes of (Z3)^2 and (Z4)^2.
3 being a prime number, Z3 is a field, (Z3)^2 a vector space, and every subgroup a sub-vector space. Hence, since the isomorphy class of a vector space is determined by its dimension, we have the following isomorphy classes of subgroups in (Z3)^2: {0}, Z3 and (Z3)^2.
In (Z4)^2 we have the following isomorphy classes of subgroups: {0}, Z2, Z4, (Z2)^2, Z2 x Z4 and (Z4)^2.
Thus, for subgroups in (Z12)^2 we have 3*6 = 18 possible combinations to form a direct sum, and hence 18 isomorphy classes of subgroups. This classification is, of course, rather rough; but there is a possibility that it can be used in combination with some of the other methods - namely to tell apart non-isomorphic motifs that have identical voulme and subset classes.
Again, I let the computer do this for all examples of Köhler's list. The result was: with the range invariant we do NOT get a refinement of the classification with volume and 3-element subsets.
For motifs with at least 4 elements, the subset classification can be refined in the following way: an isomorphy transformation will not just map 3-element subsets into isomorphic 3-element subsets, it will also map every intersection between those subsets into an intersection between the transforms (also isomorphic, of course). This means that two motifs having the same isomorphy classes of 3-element subsets might still show a different distribution of the classes on the intersecting points.
This idea can be visualized as follows: We draw a point for every 3-element subset and a connecting line between any pair of points. For 4-element motifs, the resulting figure will be a tetrahedron. The "simple" subset classification can then be imagined as painting every corner with a colour according to the isomorphy class of the corresponding subset, while for the "refined" subset classification we also paint every edge with a colour according to the isomorphy class of the 2-element intersection of the corner sets - and a necessary condition for isomorphy of the motifs is that the such painted tetrahedrons look exactly the same (up to the ordering of the corners, of course).
I will make some examples to illustrate this.
1. Let the motif be m:= { (0,0), (0,1), (1,0), (1,1) }.
As can be checked easily, for all 2-element subsets of m the gcd of the parameter differences is 1, and for all 3-element subsets the volume is 1.
From this follows at once that all corners as well all edges of the tetrahedron will have to be painted in the same colour, and hence in this case there is no refinement possible.
2. Let m := { (0,0), (0,1), (2,0), (4,7) }. It has the following 3-element subsets:
{ (0,0), (0,1), (2,0) }, { (0,0), (2,0), (4,7) } both with volume 2 and subclasses 1, 1, 2
{ (0,0), (0,1), (4,7) }, { (0,1), (2,0), (4,7) } both with volume 4 and subclasses 1, 1, 2
The tetrahedron looks as follows

We see that from every corner there have to part 2 edges with class 1 and one with class 2. Geometrically, there is another possible constellation with the same "simple" subset classification:
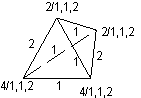
Hence, in this case we might have the possibility to tell two classes apart; but whether this variant actually occurs is another question.
This refinement works the same way for motifs with 5 and more elements - except that there we have to deal with simplexes of more than 3 dimensions.
To see whether there are several possibilities is rather complicated for a computer (it could be done using Polya's theory of combinatorial enumeration), but - at least for 4-element motifs - quite easy for a human being. This time, I did the examination manually – restricting myself to the cases that are left ambiguous from the volume/subset method.
From the examples above one can imagine that in many cases the possibilities to "glue together" the corners of the tetrahedron are quite limited. More precisely: of the cases I examined, in ALL EXCEPT ONE there is only one possibility to glue together the corners! The only case with 2 possibilities is the case I described above - and unfortunately the second case does not occur.
Thus, the invariants "range" and "refîning the subset classification" are not helpful for the special case of motifs with 4 elements in (Z12)^2. I described them nevertheless - first, because a negative result is still a result, and second, because they might help in other cases (more elements or other measures).
| Go top | ||
| © Hans Straub, 1999 | Previous: Mathematics, part 2 - Index - Next: Mathematics, part 3 |