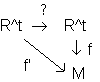
Contributions to module-theoretic classification of musical motifs
| Index Previous Next |
Mathematics, part 3 |
In this chapter I will describe another invariant that will enable us to do the complete isomorphy classification of arbitrary motifs in (Z12)^2 and some other measures (not in all, though).
Let again be R the ring Z or Z12 and M be an R-module. let m = {v0, v1, ..., vt} be a set in M with t+1 elements. Now we define the mapping
f: R^t ® M, ei ® vi-v0
where e1, e2, ... et form a basis for the R-module R^t. f is an R-module homomorphism from R^t to M. Its range is our previously described "Rm" (so you know now why we called it "range"). The kernel of f (the elements of R^t whose function value is zero) is a submodule of R^t. Now, what happens to the kernel if we apply an affine transformation to the motif m?
If we apply a translation, the mapping f will be identical since f'(ei) = (vi+w)-(v0+w) = vi-v0 = f(ei)
If we apply an automorphism g of M the transformed mapping will look like this:
f'(ei) = g(vi-g(v0) = g(vi-v0) = g(f(ei))
i.e. f = g f (the concatenation of f and g). As we showed in the chapter where we introduced Rm, the range of gf is isomorphic to the range of f; the kernel of gf, in contrary, is even IDENTICAL to the kernel of f!
However, what the kernel does depend on is the ordering of the elements of m. So we will now have to examine the effect of a permutation of the elements.
Let now s be a permutation of the set {0, 1, ...t }. Then we get the mapping
f'(ei) = vs(i)-vs(0)
How do the mappings f and f' hang together?
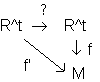
What we are looking for is a linear mapping from R^t to R^t - which we will designate with Ñs - for which holds: f' = f Ñs (making the diagram commutative); i.e.:
| f(Ñs(ei)) | = f'(ei) = vs(i)-vs(0) | |
| = (vs(i)-v0) - (vs(0)-v0) | ||
| = f(es(i)) - f(es(0)) | (if s(i) ¹ 0 and s(0) ¹ 0) | |
| = f(es(i) - es(0)) |
If s(i) is 0 (this is the case for exactly one i) es(i) is not defined. But in this case vs(i)-v0 is 0, and we can save us a separate formula for this special case if we define (as a pure convention):
e0:= 0 (zero vector in R^t).
Then f(e0) vanishes, too, and for the mapping Ñs we get the following formula:
Ñs(ei) = es(i) - es(0).
For the simple case where the permutation s just exchanges the element 0 with another element k (in cycle notation: (0 k)), we get:
| f(Ñs(ek)) | = - (vk-v0) = f(-ek) | Þ Ñs(ek) = -ek | |
| f(Ñs(ei)) | = (vi-v0) - (vk-v0) = f(ei-ek) | Þ Ñs(ei) = ei-ek | for i different from k |
Hence Ñs is described by the following (t x t)-matrix:
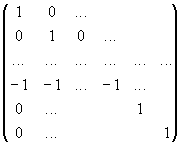 (the
-1 in the k-th row)
(the
-1 in the k-th row)
This matrix's determinant is -1, i.e. the matrix is regular, the mapping has an inverse, and
Ker f' = Ker (f Ñs) = {v in R^t, such that Ñs(v) is in Ker f}= (Ñs)-1(Ker f).
If s is an arbitrary permutation, it can be composed of simple permutations of the form (0 k), and there holds
The proof for this is straightforward (I have done it in detail in my original work, but I will skip it here). So what we have here is a representation of the permutation group as a matrix group in GL ( t, R ).
We have now established a connection between subsets of the R-module M with t+1 elements and orbits of submodules of R^t with respect to a certain matrix group. So far, this is just another invariant - but it turns out that for the case R = Z12 and M = (Z12)^2 this invariant determines the isomorphy class for any t COMPLETELY! This is the essence of the following theorem.
Let R be Z12. Let t be an integer and K1 = {x0, x1, ..., xt}, K2 = {y0, y1, ..., yt} two sets of R^2 with t+1 elements. As in the previous section, we define linear mappings:
f1: R^t ® M, ei
® xi-x0
f2: R^t ® M, ei
® yi-y0
Then holds:
| K1 is isomorphic to K2 if and only if there is a permutation s of the set {0, 1, ...t } such that Ñs(Ker f1) = Ker f2 |
(As throughout this website, I merely sketch what I did in detail in my original work. Since this is a central theorem of the work, I give some more details.)
The first part of the proof ("Þ") was outlined in the first section of this chapter. Now I sketch the second part ("Ü") .
We write Fk := Ker fk (submodules of R^t), RKk := Range fk (submodules of R^2). Let s be a permutation such that Ñs(Ker f1) = Ker f2. Since Ñs is in Gl(t,R), F1 is isomorphic to F2.
| fk | |||
| R^t | ® | RKk | |
| p | ¯ | ||
| R^t/Fk |
(p is the canonical projection.)
The dashed line defines a function f'k via: f'k([x]) := fk(x). This function is well-defined and an isomorphism from R^t/Fk to RKk. There holds: f'1([ei]) = xi-x0, f'2([ei]) = yi-y0.
| p1 | |||||
| F1 | Ì | R^t | ® | R^t/F1 | |
| ¯ | Ñs | ¯ | Ñs' | ||
| F2 | Ì | R^t | ® | R^t/F2 | |
| p2 |
We want a mapping Ñs' such that the diagram commutes.Claim: Ñs' is well-defined and an isomorhpism from R^t/F1 to R^t/F2.
Proof:
Ñs'([x]) = Ñs'(x + F1) = Ñs(x + F1) = Ñs(x) + F2 = [Ñs(x)].
Ñs' is a homomorhihsm; it
is surjective since Ñs and
p2 are.
[x] = 0 Û x Î
F1 Û Ñs(x) Î F2 Û [Ñs(x)]
= Ñs'([x]) = 0. Hence Ñs' is injective.
(Since R is finite in our case, injectivity implies
surjectivity.)
| f'1 | |||||
| R^t/F1 | @ | RK1 | Ì | R^2 | |
| Ñs' | ¯ | ? | |||
| R^t/F2 | @ | RK2 | Ì | R^2 | |
| f'2 |
Both the mappings f'k as Ñs' are isomorphisms and hence have inverses. We make the diagram commutative with the mapping
f'2 Ñs' (f'1)-1=: a
a is an isomorphism from RK1 to RK2, and
a(xi-x0) = f'2 Ñs' (f'1)-1(ei) = f'2(es(i)-es(0)) = ys(i) - ys(0)
Now we are nearly finished. Observe that the mapping a, combined with appropriate translations, yields an affine transformation that indeed maps K1 to K2! a has but one single flaw: it is not an automorphism of R^2 but an isomorphism between 2 submodules of it. The remaining task is now to find an automorphism a' of R^2 whose restriction to K1 is a (or a' is an extension of a).
On first sight, this may seem trivial - actually, it were close to trivial if R^2 were a vector space. But for general modules or groups, it is a priori not clear whether such an automorphism exists at all! This question, BTW, is addressed in a theorem which is known as the Fitting Lemma. (Look in standard literature for more information.)
Here (at least for now) I just state that in the special case of abelian groups all whose p-components have the form Zn^k with n a power of p, any isomorphism between 2 subgroups can always be extended to a group automorphism. (Actually, I have proved this in detail in my original work - but again, at least for now, I skip the details here...)
So, with this theorem at hand, the classification of musical motifs in Z12^2 up to isomorphy is completed!
| Go top | ||
| © Hans Straub, 2003 | Previous: Classification, part 4 - Index - Next: Classification, part 5 |