Parametrization explained: to be prepared


As mentioned at several points in the main page, parametrization of Kimballs model is necessary for getting rough ground state energies and reasonable structures. However, for Kimball and his doctorands the main issue had been to understand the working of chemical bonding with a simple, quantitative model, not precision! For a (possible) "user", I felt it important to validate the model: If calibrated with experimental data or good first principles computations, can it converge to represent what we know about the structure and energetics of a molecule? If so, is it possible to transfer calibration from few molecules to whole classes of chemical compounds, such that a small number of parameters correctly represents a large body of chemical knowledge? In order to make this endeavor transparent I present some examples:
1. shows the series LiH ... HF with Kimballs "parameters" as first computed by L.M.Kleiss, loc.cit. 		main page. She presented the total energy of the molecules and the radii of the electron clouds, but omitted the atomization energies, based on the experimental atomic energies. Look at the mean thermodynamic bond energy (0 K) in the tables: This is the atomization energy of the molecule divided by the number of bonded hydrogens. A positive number signifies a bond, a negative number an unstable situation. Obviously, only BH3, CH4 and NH3 are calculated to be bonded - the rest is unstable in regard to atomization to experimental atoms. The lower two tables show the same data parametrized with G3/6-311+G(d) computations, and are within the uncertainties of experimental values. This suggested to me, that Kimballs "Ansatz" could be applied, if many more tests gave similar results. That is, what we did in the sixties of last century and came to an affirmative answer, using experimental data for calibration!
  1. Necessity of parametrization: LiH ... HF again, table
  2. Example for a run with Paramki: CH4, and result
  3. Parameters along the series LiH ... HF, Regularities
  4. Parametrization of spherical shells with FDA, as used for atoms beyond K
2. gives program and output for the parametrization of CH4. The program is runnable (e.g. in DOSbox) and contains all the details. Here is the output of the equivalent Mathematica code.- This is one example of some 100 similar files for as many molecules, downloadable as zip from paramki.
3. puts the four parameters of CH4 (k1,k2 kinetic energy for R1 and R2, σ1, σ2 for the two screening constants) found into a functional relation with Z as 		variable. Kimballs values would be 1.0 for the kin.par., 0.4 for the screenings. The repeating feature is connected to the apparition of lone pairs from N to F.
4. is a plot and fit function for the calibration of atoms beyond K with FDA. This is necessary for spherical atoms because I have not loaded Kimballs model with all the corrections that would be connected to the consideration of exchange energies from overlapped clouds.

General remarks on parametrization

First Principles Methods: The name implies that there is no calibration done with empirical data. The huge archives of basis sets which are constituents of trial wavefunctions have certainly been optimized with sets of experimental data. However, this is not parametrization, because it just helps to give the trial wavefunctions a flexibility to better and better approximate the unknown true wavefunctions of a molecule, all guided by the Variation Principle. It turns out that the linear combination of Atomic Orbitals to construct Molecular Orbitals is often not the best choice. It can be defended because the complete set of spherical AOs represents an orthonormal set which asymptotically can approximate every (well-)behaved function, hence also an MO. The usual chemists' jargon with LCAO-MO arguments, however, truncates these infinite expansions at the first term(s) which is(are) far from any "optimized wavefunction". At the beginning of QC, computers were not capable of doing much better. Today this has changed dramatically. Fast computers have also opened a way to use other orthonormal function sets: One of them are planewaves, e.g. eikr, cosine and sine functions. The famous Car-Parrinello code as realized in the CPMD program package, entirely works with these. The method makes use of the existence and applicability of algorithms for Fast Fourier Transformation FFT. Together with Pseudopotentials, summing much of the contribution of low lying core orbitals and with the help and advantage of DFT functionals this has become the method of choice to follow dynamic trajectories even of large chemically reacting systems. It is amazing how much we have learned from this method in the last 20 years. Chemists may wonder when they see familiar energy level and orbital surface plots which are not derived from atomic orbitals, but computed from planewaves: The picture shows a density surface for B2H6, computed with more than 500'000 plane waves in 3 min on my home computer. Since 1960 (S.Golden, Rev.Mod.Phys. 32(322-327), and 1987 (W. Yang, Phys.Rev.Lett.59,1569-1572) DFT functionals without any orbitals have been developed. So, why stick to atomic orbitals for representing molecules?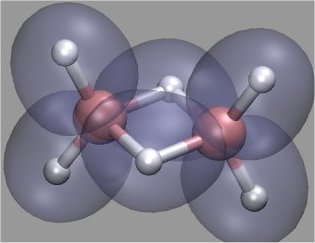
Every molecule is a new entity and not (accurately) derivable from its atoms - atoms are not bricks, molecules not houses (none of the many schemes to parse molecular electronic density into atomic contributions can be realized without arbitrary assumptions. Deep down, NMR shows more and more atomic character because a large part of the interaction with nuclear spins happens in a fairly shielded assembly of spherical <ns2> core densities).- In the last 20 years John Pople and his crew (citaton), and later without him, have developed the combination QC methods Gaussian G1, G2, ... ,G4. The aim is to reach "chemical accuracy" for enthalpy of formation, ionization potentials, electron and proton affinities. This has been an heroic undertaking. I've followed and used it carefully, because I was applying this for parametrizing Kimballs model. The methodology made great progress and is now within about 0.5 - 1.0 kcal/mol of experimental formation enthalpies with excellent predictive capability. But, a final correction determined with a large basis of experimental data, i.e. parametrization called "highher level corrections" in Gaussian09™, is still necessary. For CH4 it amounts to about 1/4 of one CH bond energy! G3MP2 is now offered in Gamess as well.
Semiempirical Methods: They range from modestly parametrized methods, e.g. Roald Hoffmann's EHT, to Allinger's (a.m.o.) empirical Force Field models with huge parameter libraries. Most of these can only give partial results. EHT cannot determine optimized structures nor ground state energies, because electron repulsion is neglected. The merits of these and dozens of other QC methods is well described in Frank Jensen, Introduction to Computational Chemistry, 2nd ed, 2006, ISBN-13:978-0-470-01186-7. I have been studying the codes of many QC programs, to discover in what way parametrization has been done (and perhaps hidden!), in order to learn, how I could proceed with Kimballs model.