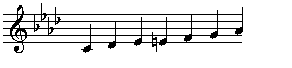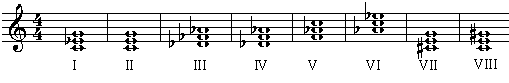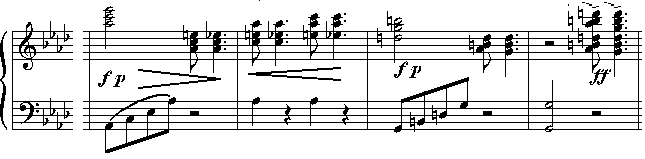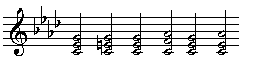On-To-Sû, So-Na-Ta

The basic idea to my composition "On-To-Sû, So-Na-Ta" was born when I was reading an article by Daniel Muzzulini [2], which describes a generalization of Mazzola's mathematical model of musical modulation [1] to arbitrary 7-element scales in equal temperament and tries to deduce a particular position of the most common scales used in classical music - with arguments that in many aspects didn't convince me.

One possible way to find hints to answers of questions raised in Muzzulini's report such as: what exactly distinguishes the diatonic major scale from any arbitrary one, or: what exactly is the musical relevance of Mazzola's mathematical structures, is to apply the theory. So I chose a harmonic structure differing slightly from classical theory and started experimenting with it.

The piece "On-To-Sû, So-Na-Ta" is a result of this experiment - but most of all, so I would like to emphasize, it is music. I didn't even bother so much about the theory - after a certain time of experimenting a was partly able to proceed without "calculating" (the piece was more or less composed the "traditional" way). This is why an analysis of the modulations with Mazzola's theory might give some additional insight - especially to the question whether the coincidence between theory and practice is as high as in the case of the diatonic scale. I intend to do this, but I haven't found the time yet. (For more informations about Mazzola's theory of musical modulation see [2]or [4].)

Just to listen:

Since the underlying harmonic structure differs only slightly from classical harmonics, the piece is more or less listenable without knowledge of the theory (although whether you like it or not is, of course, a matter of taste...); here is the COMPLETE MIDI FILE.

However, the probability is rather high that you will have difficulties to hear exactly where the modulations occur. A little hint: the piece is in the form of a classical sonata movement - a form which pre-defines some of the places where modulations should occur, and which is strictly observed here, especially in the exposition.

More detailed explanations:

Description of the harmonic structure "On-To-Su, So-Na-Ta" is based on:
Harmonic analysis of selected parts (with MIDI samples)

Harmonic structure "On-To-Sû, So-Na-Ta" is based on

The music notation samples in this chapter were created using the cappella notation software.

Definition

First I chose a scale (more precise: a pitch class set) that is, instead of the diatonic major scale, to serve as a base. (According to the numbering in [1] and [2], it is no. 50.)

From all the harmonies and disharmonies that can be created with pitches of this scale, I defined a basic set that are mainly to be used (a kind of analogon to the classical triads I, II, III etc.). I used the following (arbitrary) definition:

All 3-element subsets of the scale that have the structure of a major, minor, diminished or augmented triad.

These are the following 8 triads (numbered arbitrarily):

Transposing the basic scale and the triads, we get 12 "keys" or "tonalities": other scales of the same structure and the chords belonging to them. The word "key" (or "tonality") is in this context defined as follows: a musical phrase is in one "key"/in one "tonality" if its harmonies are built on triads of one transpose of the basic triad set.

With that, the harmonic foundation for "On-To-Sû, So-Na-Ta" is already complete! If we want, we can at once go over to the piano... One of the appealing properties of this definition is its simplicity.

Cadencial sets

As first orientation in the new harmonic realm, the concept of cadence-set is very helpful. Our structure has 12 minimal cadence-sets - which places it between the diatonic (5) and the harmonic minor scale (21). The minimal cadence-sets in detail are:

{Db-}
{Cm, C+}
{Cm, Fm}
{Cm, Dbm}
{Cm, Db}
{Ab, C}
{Ab, Fm}
{Ab, Db}
{C, Dbm}
{C, Db}
{C+, Db}
{Fm, Dbm}

Neutral triads

A counterpart to cadence-sets are neutral triads, i. e. those that cannot be uniquely assigend to a certain tonality. Schönberg's modulation model gives them, of course, importance for phase I! The more neutral triads we have, the bigger is the variety of possibilities to modulate - the number of common elements can, BTW, be seen as a natural measure for the "distance" of tonalities. Interesting questions here are: Which tonalities do have common triads at all (those are potentially favoured tonalities for modulations), and for which tonalities is this number maximal (those are "neighbouring" tonalities).

Now let's first investigate the scales known from classical music for neutral triads. The result is another interesting duality between the diatonic (major) scale and the harmonic minor scale: every major scale has common triads with 4 other major scales, namely to those two steps in either direction on the circle of fifths. Not surprising, scales one step apart on the circle of fifths have the maximal number of common triads (4)! So the circle of fifths can be interpreted as a visualization of the distances of the major tonalities, of the "modulatory topology", so to say.
The modulatory topology for harmonic minor looks quite different. First, every harmonic minor scale has common triads with 8 other minor scales - so the modulation possibilities of harmonic minor are much larger not only concerning cadence-sets! Second, there are no unique "neighbouring" tonalities, most pairs of tonalities have the same number of common triads (2; only scales in major third distance have only 1 triad in common).

Now, how does this look like int he case of our current triad set? Here every "tonality" has common triads with 6 others; like in the case of minimal cadence-sets it is exactly between the diatonic and the harmonic minor scale. Finally, the maximal number of common triads is reached not in fourth or fifth distance, but in major third distance! The topology is different again - instead of a circle of fofths we have 3 separate "circles of thirds".

Geometric properties

If we leave out the augmented triad, we get 7 triads, namely a diminished triad, 3 major triads and 3 minor triads - exactly the same as in the classical case.

The nerve is four-dimensional. If we leave out the augmented triad, we get the following three-dimensional structure:

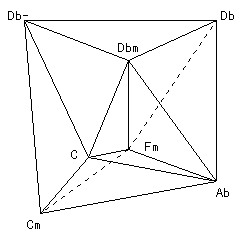
It strongly resembles the harmonic braid of the diatonic scale, but with some important differences:

Due to its three-dimensionality, it is impossible to specify a "rim" of the braid; nor is there a canonical way of ordering the triads.
The triads are not all equal.

The question is now what this means musically.

The underlying pitch-class set has - like the diatonic scale and unlike the harmonic minor scale - a non-trivial inner symmetry; in our case it is the inversion with the pitch e as a fix point. It is also a symmetry of the harmonic structure (this does not hold for arbitrary triad sets!); namely, it permutes (of course) minor and major triads while the augmented and the diminished triad stay fix. This means that for every major phrase there exists a corresponding minor phrase and vice versa, just as for every cadence-set there is a corresponding one with permuted major and minor triads.

Modes

Until now, we have treated the scale as a set, without specifying a beginning tone or triad - we have examined, so to say, only the vertical structure. When composing a concrete piece, the choice of the beginning tone/chord has importance; for that reason I add a short investigation of this subject.

Melodically, there are 7 possibilities to select a root tone; we are especially interested in those that are base tone of a major or minor triad. This condition is fullfilled by 4 tones; as a peculiarity we have 2 that are both major and minor roots. Choosing such a base tone gives you the choice of composing in major or minor or even in both at the time, which can produce some strange chromatical effects.

Since the root tone alone does not determine the character of a mode, I decided to order the modes after their base triad (so they are something like "harmonic modes"). We get 3 major modes (II, IV and VI) and 3 minor modes (I, II and V); the "chromatic" modes could be called I/II and III/IV. However, the latter appear only scarcely in the present piece.

Minor mode V is nearly a "normal" minor scale (there is only the fourth missing); as a particularity it contains both a minor seventh (like natural minor) and a major seventh (like harmonic minor). Looking a little closer from this viewpoint, the modes I and II are of interest, for the difference between mode I and mode II corresponds to the difference between natural and harmonic minor. Mode I is similar to the classical church mode phrygian while mode II reminds harmonic minor starting on fifth position (a mode that is often used in spanish flamenco music and is sometimes called spanish phrygian or spanish major).

Another mode that is comparatively close to classical music is major mode IV, whose augmented fourth gives it a lydian character. The mode corresponding to classical major (or Ionian) would be mode VI, but it lacks the dominant. Least comparable with classical music is minor mode III.

Comparison with classical harmonics

The pitch class set as well as the triad set bear quite some resemblance to classical harmonics - not too amazing, since the triad set is made up completely from classical chords. On the one hand, this made composing easy (I didn't have to "calculate" all the time); on the other hand, I was inevitably disturbed by my own musical education (which shows, e.g., in a tendency to use "classical" cadences). In the same way every listener will most probably be disturbed - missing modulations or hearing modulations where there are none.

If we try an overall comparison of chord progressions from our given triad set with classical harmonics, the nearest is harmonic minor (base tone f/mode V) - yet with important classical elements missing (such as classical IV-V-I cadences - in minor as well as in major) and, instead, a mass of chords whose base tones are at most a semitone apart - which allows the mentioned "chromatical" effects. (BTW: The augmented triad, which appears sometimes as a quite foreign element, suits in very naturally here.)

There is one point in which our harmonic structure differs fundamentally from classical harmonics (more precise: from "common-practice" classical harmonics as it was formed towards the end of the baroque era): there is no strong polarity between major and harmonic minor (this polarity uses 2 different triad sets! More information here). Since the root tone of the scale is not fixed, the musical chraracter varies with the root tone throughout the piece - more major, more minor, both or none.

Go top

Harmonic analysis of selected parts

As form a chose a classical sonata movement. This is, as I said, a form where the modulation structure is partly pre-defined; and especially in the exposition of the piece this pre-defined structure is strictly followed. This makes studying the differences to classical harmonics comparatively easy.

Exposition

Midi file: main theme of the exposition

The piece starts in mode II, the "spanish" mode - and indeed the opening motif vaguely resembles a flamenco cadence.
(Mode I and II, by the way, are the most frequent modes in the piece - the main reason for this is probably more of the psychological kind, since both have C as root tone.)
By the way, if we want to be strict, the second chord (Db-F-G) is already outside of the triad set (not of the pitch class set, though). You can see this as emphasizing my intention of making music first and experiments second. There are some more passages like this throughout the piece, but only sporadically; the basic pitch class set is never really broken - with one exception (I will come to this later).

In the phrases following the opening motif chords appear that, for "classical" ears, already seem to leave the beginning key for moments - but according to our triad definition, they stay perfectly inside. We can assume that a listener who grew up with this harmonics would hear this without problems.

Midi file: the exposition's modulation

It is more or less clear that the exposition's modulation happens somewhere in this phrase - but where exactly is more difficult: from the "classical" viewpoint, there are (at least) 3 places that come into question. First candidate is the appearing of the Ab major triad:

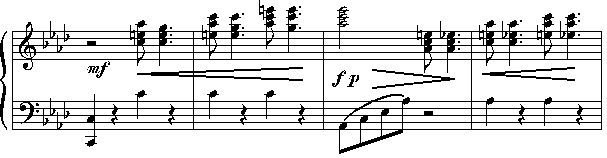(Music score samples created with cappella notation software)

But if we recall the triad definition, we see at once that the original key has not been left yet. Interesting is that the second measure sounds exactly the same as the first, since the distance between the two major triads is a major third. So what we have is a sequence of two chord progressions inside a key with a distance of a major third - a thing that does not exist in classical harmonics.

Second candidate for the key change is the appearing of the G major triad in the next measure:

And this time it happens: with G major, the beginning key is left. G major and the dircetly preceding Ab major form the cadence-set no. 10; additionally, directly afterwards we hear the diminished traid (cadence-set no. 1). The rest of the phrase - whatever one's hearing habits want to suggest - already lies completely inside the new key! The hypothetical listener who grew up with this harmonics will recognize this without difficulties.

Midi file: side theme of the exposition

The side theme starts in mode I with a quite classical sounding sequence (phrygian), followed by a short tour through the 3 major modes. The lydian character of mode IV comes out quite clearly.

Development

Midi file: another sequence with major third distance

This passage seems to modulate wildly, but in reality it stays strictly in the same key - for a listener used to this harmonics if would sound only half as wild. We have here another sequence of two chord progressions in third distance: V-II and III-VI.

"Tetrahedron" Passage

This is one of the few passages that were "calculated". When we compare the nerve of the triad set with the harmonic moebius strip of the diatonic scale, a conspicuous difference is the three-dimensionality of the former. I was asking myself how such a structure could be illustrated musically - "auralized", so to say - and was facing the problem that any chord progression always sounded "linear" to me (as the word "progression" suggests). What I did in the end was to start at one corner of the tetrahedron and go successively to each of the other corners. This results in the chord progression

for the first tedrahedron and in

for the second tetrahedron. Between the two I put a little modulation up a semitone - because of the mass of triads with root tones a semitone apart, this modulation passes very smoothly, amost unnoticed.

Midi file: development - "Tetrahedron" passage

(Well, of course, nobody will hear that a tetrahedron is described here. There might be better ways to achieve this - but here is just the explanation for that strange chord progression...)

Recapitulation

Midi file: bridge to the recapitulation

On first sight, this passage does not much stand out against the rest of the piece; but our hypothetical listener would undoubtedly notice the chord progression C-Bb which is not contained in any key. This is the only place in the piece where the underlying harmonics is out of force for a longer period.

Midi file: end of the exposition - Midi file: end of the recapitulation

Both passages contain a modulation; and on first sight, those seem to be the same: in both, there is a step from triad IV to a minor triad a fourth up (which, for classical ears, sounds like a V-i minor cadence). However, looking closer, we see that the first modulation is, as can be expected at this place in a sonata movement, a modulation down a fifth back to the tonic key while the second modulation's destination key lies a tritone apart! (This is not clear right away, but becomes so two measures later.) The fundamental step that marks the turning point is in the first case triad III, in the second case triad I. The reason for this choice of the key was here that soon afterwards there come another modulation in the opposite direction which I liked better this way (otherwise it would have sounded like this). Possibly, an analysis according to Mazzola's theory would yield a a theoretical reason for this.

Finally, once again: the COMPLETE MIDI FILE.