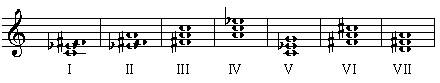The scale no. 57 (numbering according to [1]) is as follows:
From this pitch class we can construct the following major, minor and diminished triads:
Applying all possible transpositions, we get (as described on the page of On-To-Sû, So-Na-Ta) 12 "keys". The resulting harmonic structure is quite different both from classical harmonics as from the one used in "On-To-Sû, So-Na-Ta": we have 4 diminished chords with minor third distance each and 2 minor chords a tritone apart. From this follows at once that every chord set or progression made of these 6 triads is contained in the tritone-translate of the triad set and therefore can not be cadencial. So the only cadence-set is the last remaining triad, a major chord.
This is the extremest possible counterpart to harmonic minor: while the latter with its 21 minimal cadence-sets offers the richest possible choice of modulation possibilities, in our structure we have a maximum of economy and uniqueness: there is exactly one possibility to fix a certain key - there is no way past the major triad.
The question is, of course, how desirable such an extreme uniqueness is. I have the impression that composing in such a structure will rather quickly result in boredom - the classical harmonics derived from the diatonic major scale with its 5 minimal cadence-sets appears to be the better choice in the long term.
My first compositional attempts with this structure do not even sound that bad (well, at least in my ears...), which may be a certain "exotic effect", i.e. due to the strangeness of the system which possibly makes them sound more interesting than they actually are. Composing with this structure is, by the way, a little harder than with the harmonics of On-To-Sû, So-Na-Ta - I am not sure yet whether the reason lies within the structure itself or rather in its unfamiliarity.
Midi file: my first compositional attempt to scale 57 - not finished yet (latest version: 2001-03-20) and performed badly - but you can already hear the modulations.