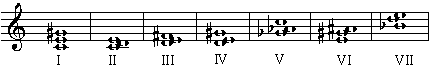The structure described below I found when I was investigating a broad range of different triad systems for 7-element scales in 12-TET. The idea behind was the question whether the polarity between the diatonic scale (5 minimal cadence-sets) and the harmonic minor scale (21 minimal cadence sets) is a property of the scale or of the special choice of triads. (The result was, BTW, that the latter holds: within certain limits, you can find triad sets with any desired number of minimal cadence-sets for every scale.)
Originally, I did not work with the whole-tone scale but with the seven-element scale that you get when you add an arbitrary tone to the whole-tone scale (this scale is unique up to transpositions; it is number 62 according to the numbering in [1] and [2]). For this scale, the maximal number of minimal cadence-sets that can be obtained with systems of 7 triads is 18 - with the slightly surprising fact that the maximum is not reached with triad sets that cover the whole scale! When I restricted the enquiry to coverings of the scale, the maximum I got was 15 minimal cadence-sets. So we have the paradox-looking situation that adding a tone leads to fewer modulation possibilities.
The maximum of 18 minimal cedence-sets is, for example, reached with the following triad definition (arbitrarily numbered):
with the whole-tone scale as carrier:
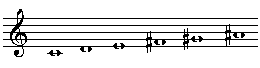
Now, a harmonic system with 18 minimal cadence-sets offers a richness of modulation possibilities that seems to come close to that of harmonic minor - not exactly what you would expect of the highly symmetric whole-tone scale! The interesting question is now whether and how this mathematics affects the music - more precisely: might this property make it possible to write whole-tone music without the notorious "amorphous" character?
Another speciality is that with this triad set we have 12 distinct "tonalities" of which 6 each have a common basic set (one of the two distinct whole-tone scales).
The symmetry group of the basic set is the full dihedron group of the regular hexagon; it has 11 non-trivial symmetries (5 translations and 7 inversions). Interesting is that none of these symmetries is a symmetry of the triad set: the triad set is rigid. Looking at the individual triads does not even seem to suggest this very much (there are 3 symmetrical chords and 2 pairs whose translation classes are mapped onto each other under inversions) - but it becomes evident rather quickly when we bear in mind that a symmetry must leave the only augmented triad (number I) invariant, which already limits the choice of candidates considerably.
As for melodies, we are left with the whole-tone scale, which means there are no "modes" in the known sense of the word - the beginning tone does not seem to matter. I say "seem to" - since in reality it does matter a lot, as soon as the harmonies come in. The pitches F# and A# are each only part of two triads - while six of them contain the pitch E! The pitch E sort of dominates the harmonic structure and hence appears to be a natural choice as a basis.
Music based on the structure is starting to form; but I am still im the experimental stage. The mentioned "amorphous" character of the whole-tone scale, by the way, seemed first not willing to let itself chase away: all chords somehow sounded alike (just as "part of the whole-tone scale"). But with time, this started to change! I am quite curious how this will continue...