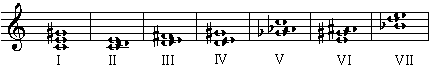Auf die unten beschriebene Struktur stiess ich, als ich für sämtliche 7-elementigen Skalen der wohltemperierten Stimmung eine grosse Anzahl verschiedener Akkordsysteme auf Kadenzmengen untersuchte. Die dahinterstehende Idee war die Frage, ob der in der klassischen Musik sich manifestierende Gegensatz zwischen Dur (5 minimale Kadenzmengen) und Harmonisch-Moll (21 minimale Kadenzmengen) eine Eigenschaft der Skala ist oder eher durch die Wahl der Stufen zustande kommt. (Das Ergebnis war übrigens, dass das letztere zutrifft: für jede Skala lässt sich durch entsprechende Wahl der Stufenmenge unterhalb einer bestimmten Grenze praktisch jede beliebige Anzahl minimaler Kadenzmengen erreichen.)
Ich arbeitete ursprünglich nicht direkt mit der Ganztonskala, sondern mit der (als Translationsklasse eindeutigen) siebenelementigen, welche durch Hinzufügen eines Tones zur Ganztonskala entsteht (Skala 62 gemäss Numerierung in [1] und [2]). Für diese Skala ergab sich bei allen Stufenmengen, die aus 7 Dreiklängen bestehen, ein Maximum von 18 minimalen Kadenzmengen - mit der etwas überraschenden Tatsache, dass das Maximum von 18 nicht mit Stufenmengen erreicht wird, welche die ganze Skala überdecken! Beschränkt man sich auf solche Stufenmengen, welche die ganze Skala überdecken, erhält man höchstens 15 minimale Kadenzmengen. Wir haben also die etwas paradox scheinende Situation, dass das Hinzufügen eines Tons zu weniger Modulationsmöglichkeiten führt!
Das Maximum von 18 minimalen Kadenzmengen wird z.B. erreicht bei der folgenden Stufendefinition (willkürlich numeriert):
mit der Ganztonskala als Grundmenge:
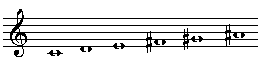
Bei einer Harmonik mit 18 minimalen Kadenzmengen ergibt sich nun eine Vielfalt von Modulationsmöglichkeiten, welche an diejenige von Harmonisch-Moll zumindest annähernd heranzureichen scheint - nicht unbedingt etwas, was man ausgerechnet bei der hochsymmetrischen Ganztonskala erwarten würde! Die interessante Frage ist nun, ob es durch diesen Trick wohl gelingt, Ganztonmusik ohne den berüchtigten "amorphen" und "strukturlosen" Charakter zu schreiben?
Wir haben ausserdem die Besonderheit, dass die Stufenmenge zwar 12 "Tonarten" aufweist, von denen aber je 6 dieselbe Grundmenge (eine der beiden möglichen Ganztonleitern) haben.
Die Symmetriegruppe der Grundskala ist die volle Diedergruppe des regulärem Sechsecks, sie hat also 11 nichttriviale Symmetrien (5 Translationen und 6 Umkehrungen). Interessanterweise führt keine dieser Symmetrien die Stufenmenge in sich über: die Stufenmenge ist starr. Die Betrachtung der einzelnen Stufen legt das nicht einmal nahe (wir haben 3 symmetrische Akkorde sowie je 2, deren Translationsklassen bei Inversionen aufeinander abgebildet werden); man sieht es jedoch relativ schnell, wen man bedenkt, dass eine Symmetrie den einzigen übermässigen Dreiklang (Stufe I) fest lassen muss, was die Auswahl der möglichen Kandidaten bereits stark einschränkt.
Melodisch haben wir, egal welchen Anfangston wir wählen, immer die unveränderte Ganztonleiter zur Verfügung. Bei Einbezug der Harmonien jedoch zeigen sich die einzelnen Töne höchst ungleich: so sind die Töne f# und a# nur in je zwei Stufen enthalten, der Ton e jedoch in deren sechs! Durch dieses geradezu erdrückende Übergewicht scheint der Ton e auf natürliche Weise zum Grundton prädestiniert.
Eine auf dieser Struktur basierende Komposition ist im Entstehen begriffen; ich bin aber noch in der Experimentierphase. Bei den ersten Erfahrungen war übrigens etwas verwirrend, dass der "amorphe" Charakter der Ganztonskala sich offenbar nicht verscheuchen lassen wollte: alle Akkorde, wiewohl verschiedener Struktur, schienen irgendwie gleich zu klingen (alles klang wie "Teil der Ganztonskala"). Mit der Zeit scheint mir jedoch, als ob sich meine Wahrnehmung zu ändern beginnt - ich bin gespannt, wie es weitergeht...