Die zu erkennenden Ziffern liegen als tiff-Dateien in verschiedenen
Grössen und Schriftarten vor. Die Abweichung von der Normallage beträgt
max. +/- 30![]() .
Es gilt eine zuverlässige Erkennung dieser Ziffern mit Hilfe von neuronalen
Netzen zu realisieren.
.
Es gilt eine zuverlässige Erkennung dieser Ziffern mit Hilfe von neuronalen
Netzen zu realisieren.
|
|
Es enhält die Schriftarten 'Times New Roman', 'Arial' und 'Comic Sans MS' in je zwei versch. Grössen.
Damit eine Spezialisierung des Netzes auf die Lehrnbeispiele verhindert werden kann, wird ein Validationset verwendet (Tabelle 3.2). Um die Generalisierungsfähigkeit des Netzes beurteilen zu können, und um das Validationset vom Trainingsset abzuheben, enthält dieses auch dem Netz unbekannte Schriftarten.
Das Validationset enthält die Schriftarten 'Script', 'Modern, 'Lucida Sans Unicode', 'Arial' mit geometrischen Verzerrungen, 'Bookman Old Style' und 'Arial' ohne geometrischen Verzerrungen. Die Ausrichtungen entsprechen nicht mehr denjenigen des Trainingsset.
Es werden folgende Merkmale aus dem Bild extrahiert und auf ihre Relevanz für die Klassifizierung gerprüft :
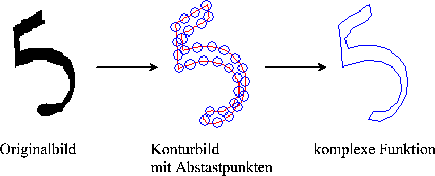 |
Diese Umwandlung erfolgt mit Hilfe der Funktionen 'ctracing' (Lit.[1], Code im Anhang B.2.1) und 'polysamp' (Lit. [2], Code im Anhang B.2.2). Die Figur wird an 32 Stellen abgetastet. Auf die so erhaltene komplexe Funktion wird nun die diskrete Fouriertransformation (Formel 3.1) angewendet3.1.
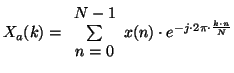 |
(3.1) |
Durch das Weglassen der Komponente X![]() (0)
und dem Normieren der restlichen Koeffizienten auf X
(0)
und dem Normieren der restlichen Koeffizienten auf X![]() (1)
sind die Koeffizienten unabhängig von der Grösse, der Position
und der Drehung der Figur. Man erhält einen Merkmalsvektor mit 30
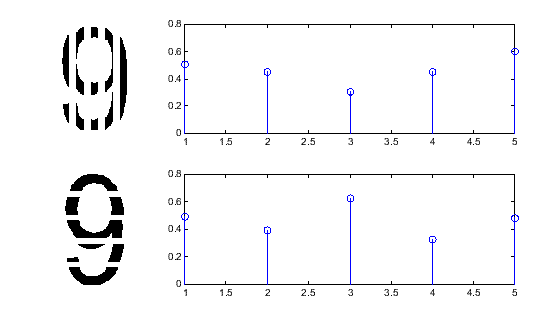
Elementen (Abbildung 3.2).
(1)
sind die Koeffizienten unabhängig von der Grösse, der Position
und der Drehung der Figur. Man erhält einen Merkmalsvektor mit 30
Elementen (Abbildung 3.2).
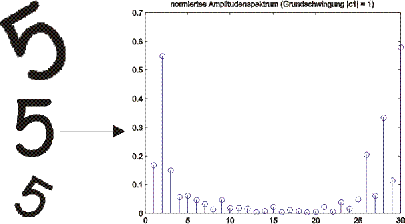 |
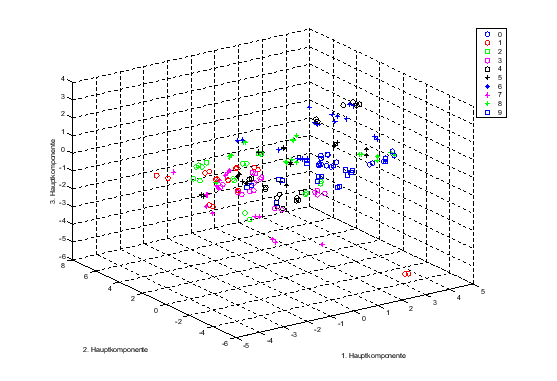
Um eine Aussage über die Klassifikationsmöglichkeiten mit Hilfe des Spektrums zu machen, habe ich die Dimension der Daten aller 180 Spektren des Trainingssets auf 2 resp. 3 Dimensionen reduziert3.2 und das Resultat graphisch dargestellt (Abbildung 3.3)3.3.
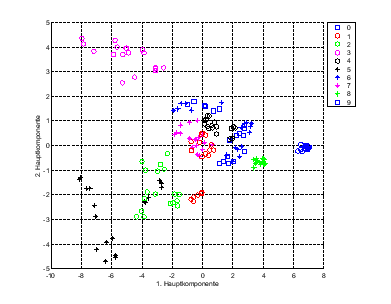 |
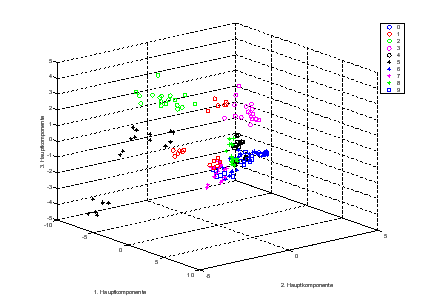 |
In Abbildung 3.3 ist zu sehen, dass
die Trennung der Ziffern 1 von 7 resp. 6 von 9 mit Hilfe der Fourierkoeffizienten
wahrscheinlich nicht vorgenommen werden kann. Dies leuchtet besonders bei
den Ziffern 6 und 9 ein, da ja nur ein normiertes, drehinvariantes Spektrum
verwendet wird.
Spätere Experimente zeigten, dass die Ziffern 1 und 7 getrennt
werden können.
Der Wert berechnet sich nach der Formel 3.2.
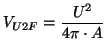 |
(3.2) |
Er ist eins, wenn das Objekt kreisförmig ist. Je mehr die "Zerklüftheit" des Objektes zunimmt, desto größer wird der Wert des Formfaktors.
Der Formfaktor ist gegen die geometrischen Transformationen Translation, Rotation, homogene Skalierung und affine Transformation mit homogener Skalierung im zweidimensionalen Fall invariant. Damit ist die Kompaktheit ein einfaches Merkmal, das wesentlich besser zur 2D Objektbeschreibung geeignet ist, als die Objektfläche oder der Objektumfang (Lit. [3]) .
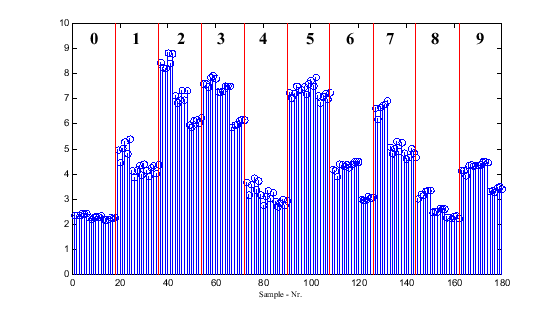 |
In Abbildung 3.4 ist zu sehen, dass der Formfaktor nicht zur Trennung der kritischen Fälle, d.h. 6 von 9 und 1 von 7, beiträgt. Da aber die Form bereits in die FFT einfliesst ist das nicht weiter verwunderlich. Der Formfaktor wird daher nicht als weiteres Merkmal verwendet.
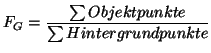 |
(3.3) |
Da hier auch Löcher in den Figuren eine Rolle spielen, kann der Füllungsgrad als weiteres Merkmal verwendet werden. Löcher verändern den Umriss der Figur nicht, und werden daher im Fourierspektrum nicht erfasst.
 |
Eine Analyse3.6 der so aus dem Trainingsset erhaltenen Daten zeigt, dass zwar eine Trennung der Ziffern 9 und 6 mit diesen Merkmalen möglich wäre, aber die gesamte Struktur der Daten das Netz wohl eher verwirren würde (Abbildung 3.6). Daher wird 6 von 9 nicht vom Netz unterschieden.
 |
Der Formfaktor und der Füllungsgrad ergänzen die beiden vorhergenannten Merkmale nur unwesentlich, und werden daher nicht verwendet.