Nächste Seite:5. Nachbearbeitung der ZiffernAufwärts:1. DokumentationVorherige Seite:3. VorbereitungenInhalt

Unterabschnitte

• 4.1 Design
• 4.1.1 Layer 1 (Eingabeschicht)
• 4.1.2 Layer 2 (Ausgabeschicht)
• 4.2 Training
• 4.2.1 Automated Regularization
• 4.2.2 Levenberg-Marquart Algorithmus

4. Das Netzwerk

4.1 Design

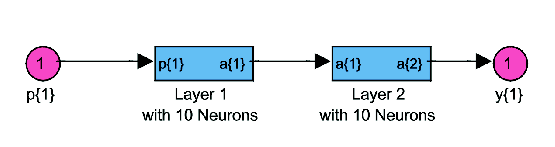
Die Analyse der Merkmale hat gezeigt, dass die Eingabedaten für das Netz eine relativ einfache geometrische Struktur aufweisen. Für die Klassifizierung der Daten habe ich mich daher für ein Backpropagation-Netz entschieden. Versuche haben gezeigt, dass 2 Schichten für dieses geometrische Problem ausreichend sind. Abbildung 4.1 zeigt die Struktur des Netzwerks.

Abbildung 4.1: Netzwerk

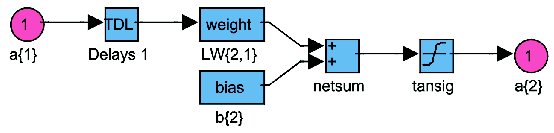
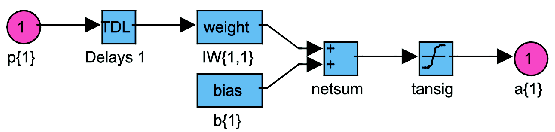
Als Transferfunktion wird in beiden Schichten 'tansig' verwendet (Abbildung 4.2). Diese Konfiguration zeigte bei den Experimenten die besten Ergebnisse.

Abbildung 4.2: Layer des Netzwerkes

[Layer 1]

[Layer 2]

4.1.1 Layer 1 (Eingabeschicht)

Um die optimale Anzahl Neuronen in dieser Schicht zu finden, habe ich die Resultate verschiedener Konfigurationen miteinander verglichen. Die Ausgabeschicht (Layer 2) war dabei wie in Kapitel 4.1.2 beschrieben konfiguriert.

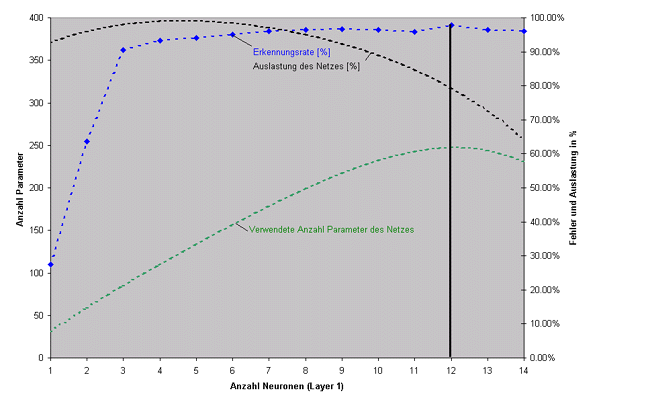
Die Resultate dieser Versuche sind in Abbildung 4.3 in dargestellt^4.1.

Abbildung 4.3: Auslastung von verschiedenen Netzarchitekturen

Die besten Resultate liefert ein Netz mit 12 Neuronen in der ersten Schicht. Bei dieser Konfiguration werden 80% der Netzparameter verwendet.

4.1.2 Layer 2 (Ausgabeschicht)

Die Ausgabeschicht (Layer 2) hat die Dimension 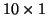$10\times 1$. Jedes Neuron repräsentiert somit eine Klasse (Abbildung 4.4).

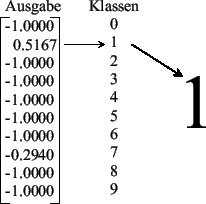
Wird die Ausgabe auf diese Art codiert, zeigt das Netz bessere Klassifikationsleistungen als bei einer Codierung mit nur einem Ausgabeneuron (siehe dazu Lit. [4] ). Als 'aktiv' gelten Neuronen mit einem Ausgabewert von > 0,5^4.2 .

Abbildung 4.4: Ausgabe des Netzwerkes

[Klassifizierung möglich]

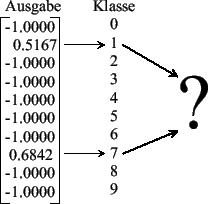
[Klassifizierung nicht möglich]

4.2 Training

Ich studierte das Verhalten von zwei verschiedenen Trainingsalgorithmen.

Es hat sich gezeigt, dass 'trainbr' (Kap. 4.2.1) in diesem Fall leistungsfähiger ist als 'trainlm' (Kap. 4.2.2).

4.2.1 Automated Regularization

Das Training mit diesem Algorithmus hat zwei Hauptvorteile :

1. Es liefert Informationen über die Auslastung der Parameter des Netzes. Dies gibt wertvolle Informationen darüber, ob das Netz richtig dimensioniert ist.
2. Mit diesem Algorithmus kann man das Netz nicht übertrainieren. Daher braucht es kein Validationsset. Das vorhandene Validationset fungiert hier als Testset, um die Generalisierungsfähigkeit des Netzes zu beurteilen.

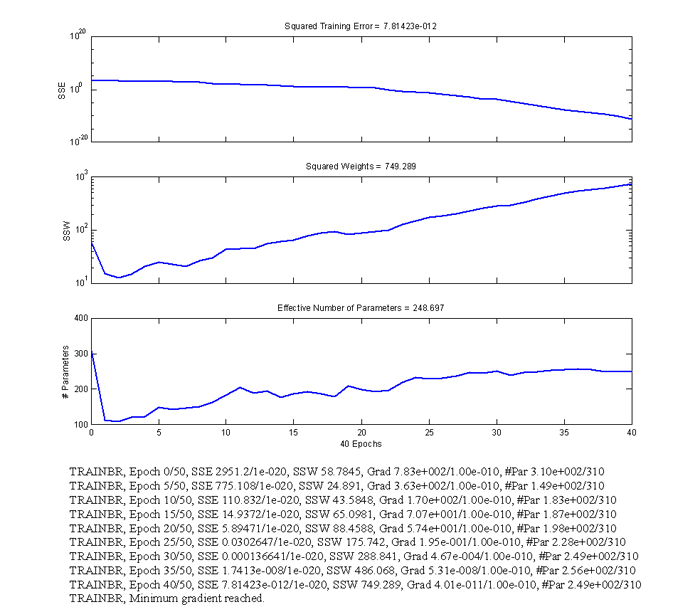
Abbildung 4.5 zeigt die Informationen, die MATLAB zum Trainingsvorgang liefert.

Abbildung 4.5: Training des Netzes mit 'trainbr'

Das mit dieser Methode trainierte Netz liefert folgende Resultate^4.3 :

Eine weitere gute Eigenschaft ist, dass praktisch jeder Trainingsdurchlauf ein gut konditioniertes Netz liefert.

4.2.2 Levenberg-Marquart Algorithmus

Hier habe ich für das Training der Gewichte den Backpropagationalgorithmus nach Levenberg-Marquardt verwendet^4.4, die Biases wurden mit Hilfe der Gradientenabschtiegsmethode mit Momentum berechnet^4.5.

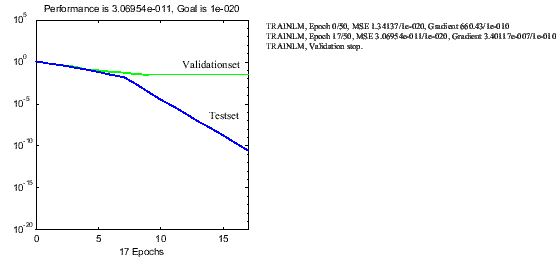
Um eine Spezialisierung des Netzes auf das Trainingsset zu verhindern, wurde das Training abgebrochen, wenn der Fehler auf dem Validationset wieder anzusteigen begann. Diese Methode ist als 'Early-stopping'' bekannt und wird von der MATLAB-Funktion 'train' unterstützt (Abbildung 4.6).

Abbildung 4.6: Trainig des Netzes mit 'trainlm' (early stopping)

Das trainierte Netzwerk liefert folgende Resultate^4.6 :

Die in Kapitel 4.1.1 ermittelte Anzahl Neuronen lieferte hier nicht die besten Resultate. Für 'trainlm' waren zu viele Freiheitsgrade im Netz, was zu einer schlechten Verallgemeinerungsfähigkeit führte. Versuche zeigten, dass 10 Neuronen im Layer 1 die besseren Resultate bringen.

Die Resultate bleiben aber trotzdem noch hinter denen von 'trainbr' zurück. Es wurden auch mehr Versuche benötigt, bis ein gut konditioniertes Netz gefunden worden war.

Ein kleiner Vorteil liegt darin, dass weniger Neuronen verwendet werden. Das Netz benötigt somit etwas weniger Speicher, was aber in dieser Grössenordnung und bei den heutige Systemen kaum mehr eine Rolle spielt.

2001-02-25