Nächste Seite:6. ApplikationAufwärts:1. DokumentationVorherige Seite:4. Das NetzwerkInhalt

5. Nachbearbeitung der Ziffern

Das normierte Amplitudenspektrum erlaubt keine Trennung der Ziffern 6 und 9 voneinander (siehe dazu Kapitel 3.1.1). Es existiert daher nur eine Klasse für diese beiden Ziffern. Wird ein Muster dieser Klasse zugeordnet, ist eine Nachbearbeitung erforderlich.

Versuche haben gezeigt, dass weder die Projektion noch das Moment^5.1 der Ziffer gute Merkmale zur Trennung dieser Klasse sind.

Die Ausrichtung der Figur ist aus dem Phasenspektrum der komplexen Funktion ersichtlich. Zur Trennung von 6 und 9 wird daher dieses verwendet (Formel 5.1^5.2).

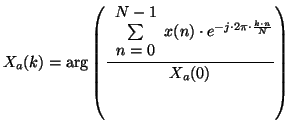$$X_{a}(k)=\arg \left( \frac{\begin{array}{c} N-1\\ \sum \\ n=0 \end{array}x(n)\cdot e^{-j\cdot 2\pi \cdot \frac{k\cdot n}{N}}}{X_{a}(0)}\right)$$ (5.1)

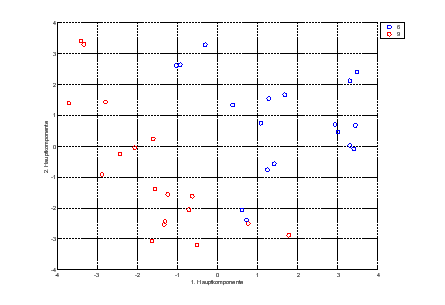
In Abbildung 5.1 ist zu sehen, dass dieses Merkmal zur Klassifizierung geeignet ist.

Abbildung 5.1: Phasenspektrum Ziffern 6 und 9 ( Hauptkomponenten 1 & 2)

Daher verwende ich auch in der Nachbearbeitung ein kleines neuronales Netz. Seine Architektur ist Analog der in Kapitel 4 beschriebenen. Einziger Unterschied ist die Anzahl Neuronen in den Schichten. Da nur zwei Klassen unterschieden werden, genügen in der Ausgabeschicht zwei Neuronen. Im Layer 1 reichen bereits 3 Neuronen aus, um dieses einfache geometrische Problem zu lösen.

Das konditionierte Netz liefert folgende Resultate :

Verrechnet mit den Resultaten des vorhergehenden Netzes (Kapitel 4.2.1) ergibt sich für die verwendeten Daten eine Erkennungsleistung > 97 %.

2001-02-25