A little thought will show you, that the tangent spherical bananas as charge clouds do not work in a quantitative Kimball model:
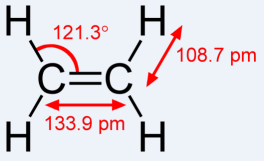
The C-C distance will be much too short: An edge of a regular tetrahedron has a distance from the center which is cos(109.47/2) = 0.57735 = 1/Sqrt[3] of the circumradius, and this is equal to the radiussum of the C(1s) + CH-clouds. Hence the C-C distance is equal to 1.1547 of the radiussum, while the C-H distance is 1.3826 of that sum (the protons are off-center for balanced forces). Hence C-C is 0.928, CH 1.111 Å (see template2 below), while Nature has CC = 1.337 and CH = 1.085 Å. With such a short distance, the bananas are not able to counterbalance the repulsion of the C+4 cores.
Hence, the C cores will be drifting spontaneously apart, as soon as you relax the unchemical condition of tangency. Bent's ethene is not stable! Perhaps the long established σ-π double bond procures just enough charge sharing to stabilize the fugitive C+4!
The HCH angle will be the tetrahedral bond angle. It should be 117.4° not 109.47°. Opening the angle is not possible without loosing the CH-clouds to be tangent on the axis containing the C nuclei.
concomittantly, the tangency of the bananas with the CH-clouds does not allow an angle of 121.3° for HCC.
If you try Acetylene as two tetrahedra with common face, Bent's model (of triple spherical bananas) is even worse: a face is tangent to the insphere and, hence, only 1/3 of the circumradius away from the center. That makes the CC distance 2/3 of the radiussum of the C(1s)+CH clouds, about 0.55 instead of 1.2 Å.
In order to attack these problems beyond mincing words we are actually doing the calculations, beginning with a literal reconstruction of J.H. van't Hoff's and G.N.Lewis' approach. This is an assignment for the reader (to be submitted at next class!). You may use the info given in the main introduction and links, and the four program templates below. Here are the exercises:
- We take two methane molecules, remove two H-atoms on both and then fuse the dangling bonds together on a common edge. For a start, the clouds' radii and all the distances are those of methane. We then compute the models energy and then let it relax under the conditions of thermodynamic and mechanical equilibrium. a) What is the outcome? b) Compare to ethene, computed with Perego's kimball.exe, see below, and c) computed with Gamess.
- If you are at it, why don't you solve the same type of problem for acetylene's triple bond? (Tip: the two tetrahedra share a common face - as you certainly have proposed by now - template3).
- next we do the case of a common vertex - ethane, where rotation of the two CH3 moieties by 60° leads to eclipsed and staggered conformations (and, hence, the internal rotation barrier as their energy difference),
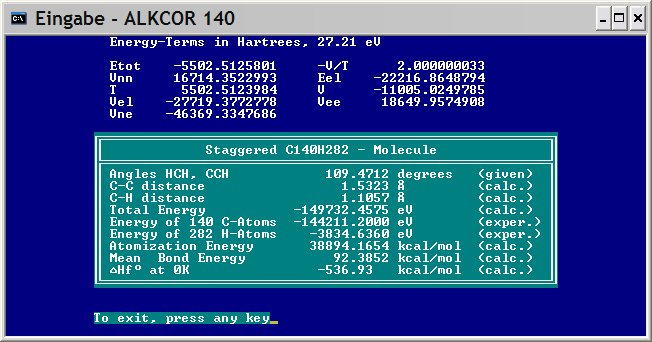
- and extend the same type of calculations to polyethenes of, say, 140 C atoms, i.e. C140H282 (see at page end)
- finally, we do diborane, where the bananas are protonated (template4).
template1 shows a methane calculation as HTML. If you want this to run, you need a Mathematica™ installation on your computer. With the Wolfram CDF Player you can "run" but not change the program. The runnable notebook is template1a.
template2 is a C2H4 computation with van't Hoff's/Lewis'/Bent's approach based on the methane results of template1. It is a Mathematica-4.0 program run that was saved as HTML. This is the runnable program.
template3 is a Mathematica program for acetylene with triple bond as common face.
template4 is a B2H6 computation with relaxed requirements for tangency, but still in the spirit of common edge tetrahedra.
If you are not familiar with Mathematica, it is very easy to translate these notebooks into any programming language from BASIC, FORTRAN to C++. I can provide a Borland Pascal variety for the same templates (and others). Mail me, click below, if you want any of them.
I'd like to motivate any reader of this Kimball site - and even more: any teacher, who exposes his students to a qualitative Kimball model and has never validated it - to try this adventure. If you get stuck and would really like to continue, I may be able to help.
Here is the result of the second to last assignment. You may download the program alk194.zip, unzip and run it in a 32-bit Windows by clicking on alk194.bat. It computes staggered, saturated C194H390 in just 12 sec on a simple computer with one CPU and produces a table similar to this one (Comment).
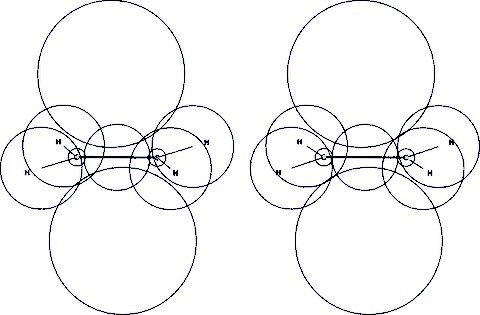 This stereo is from Perego's Kimball.exe. The input contained two C(pz) orbitals sitting at the C atoms. During the optimization the spheres fused to a π-bond in the center of the molecule, overlaps exchange corrected. Perego's energy is -77.79928 Eh
This stereo is from Perego's Kimball.exe. The input contained two C(pz) orbitals sitting at the C atoms. During the optimization the spheres fused to a π-bond in the center of the molecule, overlaps exchange corrected. Perego's energy is -77.79928 Eh
A comparison with variations on Kimball ethene is here. 1) The π-bond consists of C(pz) orbitals located above the cores. 2) Same as 1) but pz orbitals shifted towards the molecule center. 3) pz orbitals fused as in Perego's model left. It is nearest to QC results: Etot=-78.0375 Eh.
W.A.Goddard III and his coworkers have recently started a renaissance of the FSGO approach with their "Electron Force Field" method. For ethene a very interesting comparison to Kimball with practically identical dimensions results:
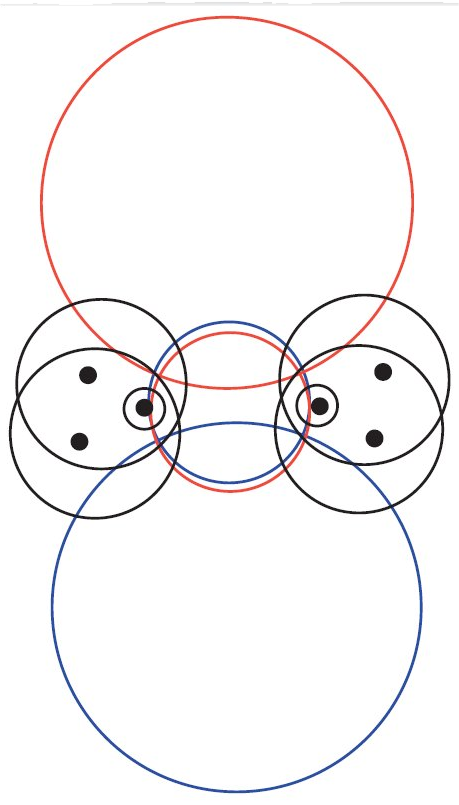 
Julius T. Su, Candidacy Report, California Institute of Technology, Feb. 28, 2003, left picture, and J.T.Su & W.A.Goddard III, JCP 131,244501,2009, Fig7, right picture. They also showed that the double banana bond is considerably less stable then the σ-π double bond. |
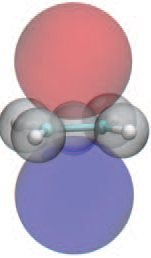
QC results: Ethene computed with Gaussian03™, model chemistry RHF/6-311++G(2d,p) opt followed by a Natural Bond Orbital analysis (NBO Version 3.1, E.D.Glendening, A.E.Reed, J.E.Carpenter, and F.Weinhold, QCPE Bull. 10(1990)58), and visualized with WebMO, 13.0.011p.- No bananas! Top: C-C π-bond, bottom: C-C σ-bond. Energy -78.059212 Eh. The Kimball model is similar, considering its simplifications.
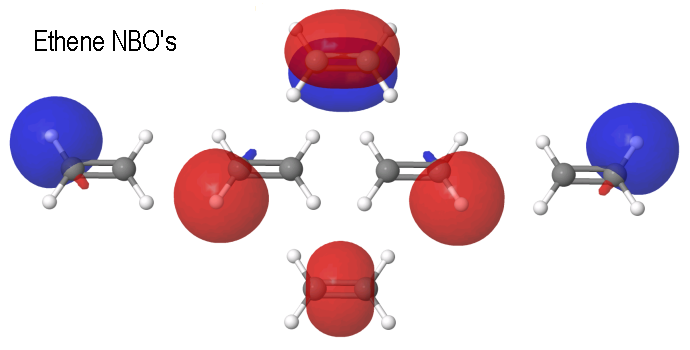
|

 This stereo is from Perego's Kimball.exe. The input contained two C(pz) orbitals sitting at the C atoms. During the optimization the spheres fused to a π-bond in the center of the molecule, overlaps exchange corrected. Perego's energy is
This stereo is from Perego's Kimball.exe. The input contained two C(pz) orbitals sitting at the C atoms. During the optimization the spheres fused to a π-bond in the center of the molecule, overlaps exchange corrected. Perego's energy is 

